Scheitelpunkt Berechnung?

Question

y=-1/3x^2+2x+3 Wie geht das, habe probiert,  kann irgendwie wie nicht.

Answer 1

Hier der Weg über quadratische Ergänzung

y = - 1/3·x^2 + 2·x + 3

y = - 1/3·(x^2 - 6·x) + 3

y = - 1/3·(x^2 - 6·x + 3^2 - 3^2) + 3

y = - 1/3·(x^2 - 6·x + 3^2) + 6

y = - 1/3·(x - 3)^2 + 6

S(3 | 6)

Comments

Hier der Weg über Formel

f(x) = - 1/3·x² + 2·x + 3 

Sx = -b/(2a) = -2/(2*(-1/3)) = 3

Sy = f(Sx) = f(3) = - 1/3·3^2 + 2·3 + 3 = 6

S(3 | 6)

Wir sehen auf beiden Wegen kommt das gleiche heraus.

Answer 2

Es gibt zig-Möglichkeiten den Scheitelpunkt
zu berechnen.

Eine davon beruht auf der Tatsache das die
x-Stelle des Scheitelpunkts in der Mitte
der beiden Nullstellen ist

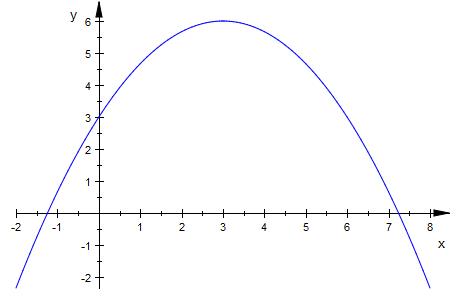
f ( x ) = -1/3x² + 2x + 3
Nullstellen berechnen
( die Mtternachtsformel könnte schon angewendet werden )

-1/3x² + 2x + 3 = 0  | * -3
x^2 - 6x - 9 = 0
( pq-Formel oder quadr. Ergänzung )
x^2 - 6x + 3^2 - 9  - 9 = 0
( x - 3 )^2 = 18
x - 3 = ±√ 18
x = ±√ 18 + 3

Nullstellen
x = + √ 18 + 3
x = - √ 18 + 3
Mitte der Nullstellen
[ ( √ 18 + 3 + ( - √ 18 + 3 ) ] / 2
xs = 3

Comments

Wenn die Nullstellen bei 

x = a ± √b

sind, wo ist dann eigentlich die Mitte davon?

Muss man da

xs = 1/2 * (a + √b + a - √b)

rechnen oder ist das vielleicht gleich

xs = a

---

Aus pädagogischen Gründen habe ich
etwas ausführlicher geantwortet.

Außerdem bin ich ein Typ von dem
es heißt
Verliert er im August die Hose war im Juli
das Gummiband schon lose.

Answer 3

-1/3*(x^2-6x+3^2-3^2)+3  (Quadratische Ergänzung zu einer binomischen Formel)

-1/3*(x-3)^2 +3+3 = -1/3*(x-3)^2+6

--> S(3|6)

Alternative:

1. Ableitung Null setzen (falls du weißt, was eine Ableitung ist)

Dann gefundene Stelle einsetzen, um y-Wert zu berechnen.

y'= -2/3x+2 = 0

--> x=3 --> y(3)= 6

Comments

Hallo Andreas,

-1/3*(x²-6x+3²-3²)+3
-1/3*(x-3)² -3 +3 = -1/3*(x-3)²+0

beim Ausklammern ist dir ein kleiner
Fehler unterlaufen
-1/3*(x-3)² +3 +3 = -1/3*(x-3)²+ 6
S ( 3 | 6 )

mfg Georg

---

Mann aus China schon haben ausgebesselt. Abel tlotzdem Danke sehl vielmals.

Wünschen WE schönes! :)

---

Wohin Vorzeichenfehler führen können
ist dir auch klar.

  Hier zur Aufheiterung einen Witz zum Thema : Ein BWL- ( Betriebswirtschaftslehre ), ein Physik- und ein Mathestudent wollen Ihr Zwischenexamen feiern und fliegen für ein paar Tage nach Mallorca.

  Bei der abendlichen Feier bricht im Hotel ein Feuer aus. Die
Studenten haben aus Ihrem Zimmer keinen Fluchtweg mehr.
Zum Innenhof hin liegt ein Swimming-Pool der über den Balkon erreichbar wäre.

  Der BWL-Student klettert über das Balkongitter und springt ab. Voll daneben.

  Der Physikstudent setzt sich hin, rechnet etwas, klettert übers Balkongitter
und springt ab. Mitten in den Pool.

  Der Mathestudent rechnet noch länger, klettert übers Balkongitter, springt ab
und verschwindet nach oben. Als man seine Berechnungen später fand entdeckte man :
Vorzeichenfehler. 

---

Du immel haben Witz guten auf Lager. Mann aus China Witze sehl mögen und Menschen mit Humol vielen. Weitel machen so, mein Fleund! :))

---

Nichts zu danken.
Wie immer : von Beileidsbezeugungen an meinem
Grab bitte ich Abstand zu nehmen.

---

Habe nix verstanden... Hihi:-) Was ist jetzt richtig? 

---

Es gibt doch mehrere Antworten oben die alle das gleiche Ergebnis haben. Was verstehst du nicht?

---

aso Ok, habe es übersehen, danke!