Informationen über Funktionen herausfinden (x-1)^2•(x+1)^2

Question

Brauche Informationen die ich von der Funktion ablesen kann! 

(x-1)^2•(x+1)^2

Comments

Ok, zunächst mal fehlt der Definitionsbereich der Funktion. Vielleicht ist diese Angabe untergegangen oder die Funktion ist gar nicht definiert, also auch gar keine Funktion im üblichen Sinn...

Answer 1

du kannst ablesen:

Funktion vierten Grades

Nullstellen bei x=-1 und x=1.

Ich glaube, durch die verschiedenen Nullstellen muss es Extrempunkte geben.

Mehr weiß ich auch nicht.

Gruß 

Smitty

EDIT: Die Funktion ist achsensymmetrisch zur y-Achse

Comments

Hallo Smitty,

da du dich ja auch weiterbilden willst.

f := -( x + 5 ) * ( x + 1 ) ; blau
g := -( x + 4 ) * ( x + 2 ) ; rot
h := -( x + 3 ) * ( x + 3 ); grün
oder
h := -( x + 3 ) ^2

f hat 2 Nullpunkte
dann wandern die Nullpunkte bei
g auf einander zu.
Bei h sind sie identisch

Das nennt man eine doppelte Nullstelle
= Berührpunkt mit der x-Achse.

Answer 2

Hallo Mara, 

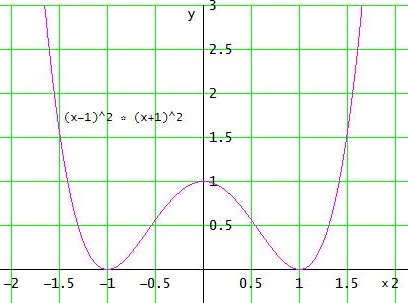
f(x) = (x-1)² • (x+1)²    mit D_max = ℝ

Die Linearfaktoren x-1 und x+1 ergeben - wenn man sie gleich 0 setzt - genau die Nullstellen x = 1 und x = -1  

Da die LF die Exponenten 2 haben, handelt es sich um doppelte Nullstellen. Deshalb sind das auch Extremstellen.  

Die Grenzwerte für x → ± ∞  sind beide ∞ , deshalb hat man dort die Tiefpunkte (-1|0) und (1|0)

f ist symmetrisch zur y-Achse  und hat den Hochpunkt (0|1)

Solche Polynomfunktionen 4. Grades  haben eine "W-form" (an den Sitzen abgerundet)

Gruß Wolfgang

Answer 3

Hier noch ein Bildchen

Comments

Tolles bild, ist oben aber schon vorhandenn. Ausserdem war das nicht gefragt.

---

Zur Verteidigung: Das Bild von Wolfgang war meines Erachtens zum Zeitpunkt von Georgs Post noch nicht vorhanden. Das hat Wolfgang nachträglich eingefügt.

Dass es nicht speziell gefragt war, ist zwar richtig, aber eine nette Ergänzung (weswegen ich persönlich es wohl nur als Kommentar zu Wolfgang gesetzt hätte, aber das ist ja jedem selbst überlassen)

---

Als Kommentar wäre das besser aufgehobe da es die eigentliche frage nicht beantwortet. Aber für kommentare gibt es ja keine punkte