Hallo
den 2 ten Teile hast du falsch aufgeschrieben. a)x>=1 x<=-1 und x>=1
1. Fall wenn x>3/2 ist x>1
also hast du für den Fall
2x-3+x2-1<=4
x2+2x<=8 quadratische Ergänzung x2+2x+1<=9, (x+1)^2<=9, x<=2 (x<=-4 fällt weg wegen x>=3/2) also: 3/2<=x<=2
jetzt den nächsten Fall
1<x<3/2, -2x+3+x^2-1<=4
so gehst du nach und nach alle aufgeschriebenen Fälle durch.
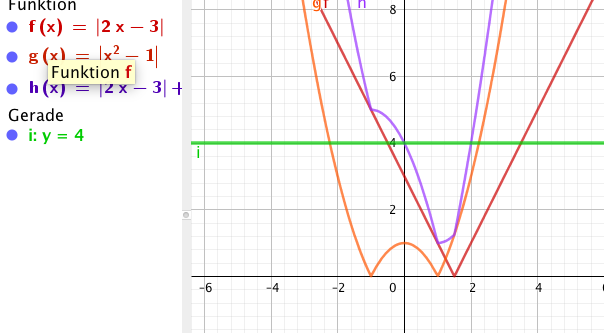
Am einfachsten sieht und kontrolliert man die Lösungen indem man die funktion skizziert, und den Teil unter 4 ansieht. siehe mein Bild
wenn du unsicher bist. poste deine Rechnungen zur Kontrolle.
Gruß lul