Polynomdivision. Bekomme nicht dasselbe Ergebnis wie die Online Rechner raus. Was ist mein Fehler?

Question

 (x^3+4x^2-11x-30):(x+3)=x^2+x-15

-(x^3+3x^2)

             x^2-11x

           -(x^2+4x)

                     -15x-30

                     -(-15x-45)

                         0 Rest 15

Comments

Könnte es sein, dass due eigentlich durch \((x-3)\) teilen möchtest?

---

Ja, habe ich vorhin bemerkt trozdem danke:-)

Answer 1

(x^3  + 4x^2  - 11x  - 30) : (x + 3)  =  x^2 + x - 14  Rest  12 
x^3  + 3x^2           
————————————————————————
        x^2  - 11x  - 30
        x^2  +  3x     
        ————————————————
              - 14x  - 30
              - 14x  - 42
              ———————————
                      12

Comments

Danke habe mein fehler gesehen :-)

---

Kontrolle auch per Polynomdivision-Rechner hier.

Answer 2

Nimmt man nicht
(x^3+4x^2-11x-30):( x+3 )
sondern
(x^3+4x^2-11x-30):(x - 3)

ergibt die Polynomdivision das Ergebnis
x^2 + 7x + 10
ohne Rest.

Comments

Was hat das mit der Frage zu tun?

Answer 3

x*3 ist nicht 4x, sondern 3x.

Answer 4

Der Definitionsbereich der Gleichung ist \(D_f=\{x≠3\}\), was sich kinderleicht ablesen lassen kann. Du hast nun die folgende Gleichung:$$\frac{x^3+4x^2-11x-30}{x+3}=x^2+x-15 \quad |\cdot (x+3)$$$$x^3+4x^2-11x-30=(x^2+x-15)\cdot (x+3)$$ Multipliziere die beiden Terme aus und erhalte:$$x^3+4x^2-11x-30=x^3+3x^2+x^2+3x-15x+45$$ Entferne gleiche Terme:$$4x^2-11x-30=3x^2+x^2+3x-15x+45$$ Fasse die Terme zusammen:$$4x^2-11x-30=4x^2-12x-45$$ Entferne wieder gleiche Terme:$$-11x-30=-12x-45  \quad |+12x$$$$x=-15  \quad , D_f=\{x≠3\}$$

Comments

Die Lösung für \(\frac{x^3+4x^2-11x-30}{x+3}=x^2+x-15\)

---

Die Antwort enthält etliche Fehler!

---

Enlighten me!

---

Oh, ich habe Polynomdivision überlesen! Ich habe den Schnittpunkt berechnet!!

---

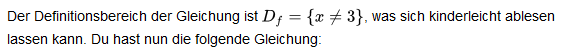
Es geht hier nicht um Gleichungen, sondern um eine Polynomdivision. Was du mit f bezeichnet hast, ist auch nicht klar, von irgendeinem f war in der Frage nirgends die Rede. Der von dir notierte "Definitionsbereich der Gleichung" (falls man den ünerhaupt betrachten muss) ist gar keine korrekte Mengenbeschreibung. Falls du damit andeuten wolltest, dass \(x\ne 3\) sein muss: Dem ist keineswegs so.

---

Ich meine damit, dass es für \(x=3\) keine Lösung gibt. Ich habe einfach nur die Aufgabe kopiert, ohne mir die Beschreibung durchzulesen.

Mein Fehler!

---

Ok, dann wird ja jetzt klar, das meine ursprüngliche Aussage wesentlich zutreffender und konstruktiver war, als meine Auflistung irgendwelcher Einzelfehler:

---

Nein, zweiteres hätte ich bevorzugt.

---

Na ja, ich wäre aber nicht auf die Idee gekommen, dass du eigentlich eine ganz andere Frage beantworten wolltest. Ich bin doch kein Hellseher!

---

Ich habe nur die Gleichung gesehen und dann angefangen zu rechnen.

---

Du hast ausklammern mit ausmultiplizieren verwechselt. Hinten muss es \(-45\) statt \(+45\) heißen.

---

Hier steht immer noch zwei mal -45 . Absicht?

Zudem: Definitionsbereich: Reelle Zahlen ohne x = - 3. Du hast da auch noch ein falsches Vorzeichen.

Ich habe nur die Gleichung gesehen und dann angefangen zu rechnen.

In dieser Gleichung ist der Definitionsbereich nicht eingeschränkt.