Ist der Abstand A'B'=h+c?
Nein - im allgemeinen Fall nicht.
s/h=c/(....) (....) verstehe ich nicht ganz, welche Länge beschreibt das.
$$\frac sh = \frac c{h+c}$$ wie schon in Deiner Frage ist \(s\) ist die Seitenlänge des ursprünglichen Quadrats im Dreieck \(\triangle ABC\) und \(h\) ist die Höhe des Dreiecks \(\triangle ABC\). \(c\) ist die Basisseite \(c=|AB|\). Und \(h+c\) ist die Höhe des großen Dreiecks \(\triangle A'B'C\) in meiner Antwort bzw. die Höhe des Dreiecks \(\triangle A'B'C'\) im Bild im Kommentar oben; bzw. \(h+c=|M_c'C|\) im Bild unten.
In dem Bild in meinem Kommentar (oben) ist \(h\) die rote Strecke des kleineren Dreiecks und \(s\) ist die im gleichen Dreieck schwarz markierte Strecke - also die Seite des eingeschriebenen Quadrats. Das Verhältnis ist in diesem Bild immer 'schwarze Strecke' zu 'rote Strecke'.
Nochmal zur Klarstellung:
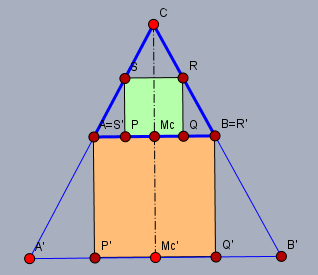
In das Dreieck \(\triangle ABC\) (dicke blaue Linie) ist das Quadrat \(PQRS\) (grün) eingesetzt - so wie in Deiner Frage.
Unter das Dreieck \(\triangle ABC\) zeichne ich ein Quadrat \(P'Q'R'S'\) (braun) derart, dass die Punkte \(A=S'\) und \(B=R'\) zusammen fallen. Ich verlängere die Schenkel des Dreiecks \(\triangle ABC\) nach unten, die die Verlängerung der Seite \(P'Q'\) in den Punkten \(A'\) und \(B'\) schneiden. Somit liegen zwei ähnliche Figuren bestehend aus einem Dreieck und einem Quadrat vor. Als einmal \(\triangle ABC + PQRS\) und zum anderen \(\triangle A'B'C + (P'Q'R'S' = P'Q'BA)\)
In beiden Figuren betrachte ich nun das Verhältnis der Seitenlänge des Quadrats \(s\) bzw. \(s'\) zu der Höhe \(h\) bzw. \(h'\) des jeweiligen Dreiecks. Da die Figuren ähnlich sind, muss dieses Verhältnis gleich sein:$$\frac {s=|PQ|}{h=|M_cC|} = \frac {s'=|P'Q'|}{h'=|M_c'C|}$$Und da ich das zweite Quadrat so gewählt habe, dass \(s'= |S'R'|=|AB|=c \) ist, setzt sich die Höhe \(h'\) des zweiten Dreiecks \(\triangle A'B'C\) aus der Höhe \(h=|M_cC|\) des ersten Dreiecks und der Seite \(|P'A| = s'=|M_c' M_c|=|AB|\) zusammen. Folglich ist$$ s' = |AB| = c\\ h' = |M_cC| + |M_c'M_c| = h +|AB|= h + c\\ \frac sh = \frac{s'}{h'} = \frac{c}{h+c}$$