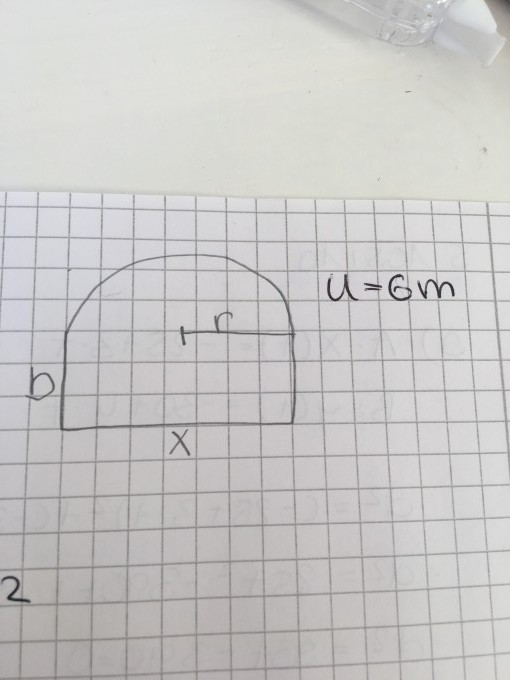
Aufgabe:
Ein Fenster besteht aus einem Rechteck mit aufgesetztem Halbkreis. Der umfang des Fensters soll 6m betragen. Für welches x wird der Flächeninhalt des Fensters am größten? Gib diesen max. Flächeninhalt an.
(X ist die unterste strecke und der halbkreis ist an ihr angebracht)
Problem/Ansatz:
Ich bin in der 9. Klasse auf einem Gymnasium also nur dass ihr wegen dem Niveau her wisst.
Alsoo ich verstehe nicht wie man da drauf kommt. Ich habs schon versucht, komme aber mit den ganzen pis durcheinander:(
Wäre super lieb wenn mir jemand helfen könnte
Lg