Hallo WASCHB4R,
Problem/Ansatz: Eigentlich die ganze Aufgabe. Angefangen mit dem Volumen ausrechnen ...
Wo genau ist das Problem. Die Formeln für das Volumen von Zylinder \(V_Z\) und Kegel \(V_K\) sind Dir sicher bekannt:$$V_Z = \pi R^2 \cdot H \\ V_K = \frac 13 V_Z = \frac 13 \pi R^2 \cdot H$$ ich habe Großbuchstaben für Radius \(R\) und Höhe \(H\) gewählt, um sie von den Größen \(r\) und \(h\) aus der Aufgabe zu unterscheiden, soweit das überhaupt nötig ist.
Kommen wir zum Volumen \(V_A\) vom Zylinder \(A\). Der Radius \(R\) ist die Hälfte vom Durchmesser \(D\).$$V_A = \pi R^2 \cdot H, \quad R = \frac D2 = \frac {2r}2 = r, \space H=h$$Jetzt ersetze die Großbuchstaben im Volumen \(V_A\) einfach durch das, was rechts vom Gleichheitszeichen der Vorgabe steht:$$V_A= \pi \left( R=r \right)^2 \cdot (H=h) = \pi (r)^2 \cdot h = \pi r^2 \cdot h$$Genauso machst Du es bei den anderen:$$\begin{aligned} V_B& = \frac 13 \pi R^2 \cdot H, \quad R=r, \space H=h \\ \implies V_B &= \frac 13 \pi r^2 \cdot h \\ V_C &= \pi R^2 \cdot H, \quad R=r, \space H=\frac 12 h \\ \implies V_C &= \pi r^2 \cdot \left( \frac 12 h \right) = \frac 12 \pi r^2 \cdot h\\ V_D &= \frac 13 \pi R^2 \cdot H, \quad R = r, \space H = \frac 12 h \\ \implies V_D &= \frac 13 \pi r^2 \cdot \left( \frac 12 h\right) = \frac 16 \pi r^2 \cdot h\end{aligned}$$Jetzt addiere die Volumen \(V_B\), \(V_C\) und \(V_D\):$$V_B + V_C + V_D = \frac 13 \pi r^2 \cdot h + \frac 12 \pi r^2 \cdot h + \frac 16 \pi r^2 \cdot h$$Du siehst, dass der Faktor \(\pi r^2 \cdot h\) immer der selbe ist. Man muss also nur \(1/3 + 1/2 + 1/6\) addieren. Das schaffst Du alleine, das ist \(=1\) und damit ist $$V_B + V_C + V_D = \pi r^2 \cdot h = V_A$$
b) Glas A wird zu 2/3 gefüllt. Mit dieser Menge wird Glas C ganz gefüllt und der Rest in Glas B gegossen. Wie hoch steht die Flüssigkeit in Glas B.
Das Volumen \(V_B'\) in Glas \(B\) ist die Differenz aus \(2/3V_A\) minus des Volumens von \(V_C\) - also$$V_B' = \frac 23 V_A - V_C$$ mache es Dir einfach, indem Du \(V_C\) und die anderen als Vielfache von \(V_A\) angibst. Es ist$$V_C = \frac 12 V_A \\ \implies V_B' = \frac 23 V_A - V_C = \frac 23 V_A - \frac 12 V_A = \frac 16 V_A $$Nun ist nach der Höhe im Glas \(B\) gefragt, was aussieht wie ein umgedrehter Kegel, also so etwas wie ein Sektglas. Oben steht $$V_B = \frac 13 V_A$$ mit dem Volumen \(1/6 V_A\) ist das Glas \(B\) also halb voll. Da das Glas \(B\) kein Zylinder, sondern ein Kegel ist, der auf der Spitze steht, muss die Füllhöhe aber höher sein, als die halbe Höhe des Glases, da unten im Glas weniger Platz ist.
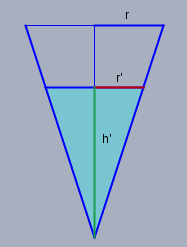
Oben im Bild siehst Du eine Skizze des Glasquerschnitts. Die Höhe der Flüssigkeit sei \(h'\) (grün) und der Radius der Oberfläche der Flüssigkeit sei \(r'\) (rot). Der untere Teil nimmt die Hälfte des Gesamtvolumens ein. Es gilt also$$ \frac 13 \pi r'^2 \cdot h' = \frac 12 \left( \frac 13 \pi r^2 \cdot h \right) $$Weiter ist lt. Strahlensatz $$\frac{r'}{h'} = \frac rh\space \implies r' = h' \frac {r}{h}$$das setze in obige Gleichung ein$$\begin{aligned}\frac 13 \pi \left( h' \frac {r}{h}\right)^2 \cdot h' &= \frac 12 \left( \frac 13 \pi r^2 \cdot h \right) && \left| \div \frac 13 \pi r^2\right.\\ \left( h' \frac {1}{h}\right)^2 \cdot h' &= \frac 12 h && \left| \cdot h^2 \right.\\ h'^3 &= \frac 12 h^3 \\ \implies h' &= \sqrt[3]{\frac 12} h \approx 0,794 h\end{aligned}$$
c) Glas C wird halb gefüllt. Diese Menge wird je zur Hälfte in die Gläser B und D gegossen. Wie hoch stehen die Flüssigkeiten in diesen Gläsern
... schaffst Du das alleine?
Gruß Werner