Aufgabe:
Die Ballonhülle des Heißluftballons wird durch horizontale und vertikale Bänder, die in die Hülle eingenäht sind, stabilisiert.
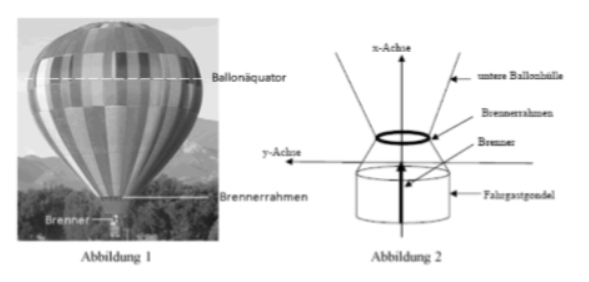
Die horizontalen Bänder verlaufen wie Fassringe rund um die Hülle. Das längste Band ist am Ballonäquator, an dem der Umfang des Ballons maximal ist. Die vertikalen Bänder verlaufen vom höchsten Punkt des Ballons seitlich hinunter bis zum runden Brennerrahmen oberhalb der Fahrgastgondel (siehe Abbildungen).
Die vertikalen Bänder werden durch die Funktion \( f(x)=\frac{x}{4} \sqrt{20-x} \) beschrieben,
wobei sich der Ursprung des Koordinatensystems an der Austrittsdüse des Brenners befindet und die x‐Achse der vertikalen Rotationssymmetrieachse des Ballons entspricht (siehe Abbildung 2).
a) Berechnen Sie die Höhe des Ballons (von der Austrittsdüse des Brenners bis zur Ballonspitze).
b) Berechnen Sie die Länge des horizontalen Bands am Ballonäquator.
c) Skizzieren Sie das Querschnittprofil des Ballons in einem Koordinatensystem.
d) Wenn man eine Funktion \( f(x) \) zwischen \( x=a \) und \( x=b \) um die \( x \) -Achse rotieren Iässt, wird das Volumen des Rotationskörpers durch \( V=\pi \cdot \int \limits_{a}^{b}(f(x))^{2} d x \) berechnet.
Berechnen Sie das Volumen des Ballons. Gehen Sie dabei davon aus, dass der Brennerrahmen 1 Meter über der Austrittsdüse des Brenners liegt.