Vom Duplikat:
Titel: eine Aufgabe zum Thema Stochastik
Stichworte: stochastik
Aufgabe 1:
Auf einem Tisch liegt ein kariertes Tischtuch. Bei einem Spiel wird eine Euromünze auf den Tisch geworfen. Bleibt sie so liegen, dass sie die Grenze zwischen zwei Karos berührt, hat die Bank gewonnen und sie behält den Euro. Der Spieler gewinnt, wenn die Münze vollständig in einem Quadrat liegen bleibt.
Aufgabe 2:
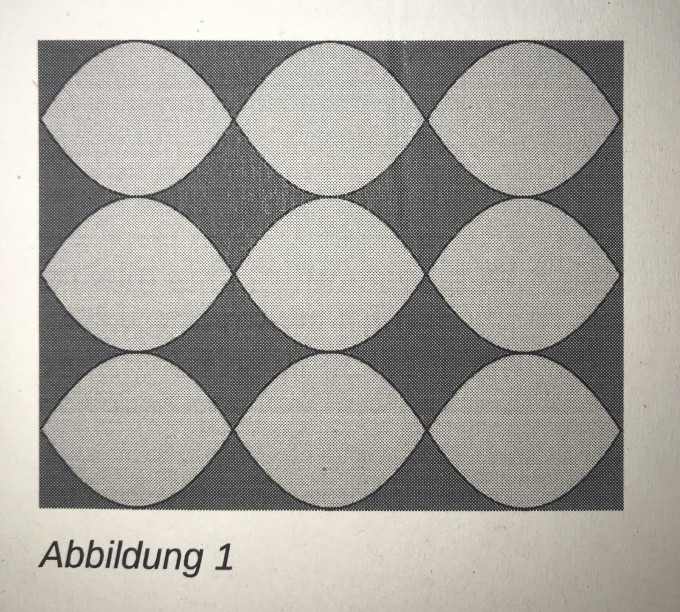
Ein zweites, rechteckiges Tischtuch ist in einem sich wiederholendem Muster gewoben, wie Abbildung 1 es zeigt. In Abbildung 2 sind die Maße für ein hellgraues Element angegeben.
Aufgabe: Betrachten sie das Spiel aus Aufgabe 1 für dieses zweite Tischtuch. Untersuchen sie, ob sich ihr Vorgehen als Aufgabe 1a) übertragen lässt.
Problem/Ansatz:
das Tischtuch ist in alle Richtungen wie in der Abbildung gemustert. In Aufgabe 1 ist nicht klar, wie groß der Tisch ist, sondern ich weiß nur wie das Muster aussieht.
Was muss man machen uns wissen, um eine Gewinnwahrscheinlichkeit abzuschätzen. Kann mein Vorgehen aus 1a) auf das neue Muster übertragen werden, oder brauch man vielleicht noch mehr Informationen oder vielleicht muss man etwas kompliziertes berechnen?
In der Aufgabe wird keine genaue Lösung benötigt. Hier die Angaben die nötig sind:
1a) = Die Gewinnwahrscheinlichkeit beträgt 0,37515626 = 37,5%
2a) = Die Auszahlung beträgt 2,67€ (vielleicht könnte das auch gebraucht werden)
Ich weiß jetzt nicht so wie ich die Aufgabe anhand mit den Angaben die Aufgabe lösen kann. Würde mich mich freuen für Hilfe (Die Abbildung habe ich hochgeladen)