Polynomfunktion Grad vier

Question

Der Graf eine Polynomfunktion f von Grad 4 hat einen hochpunkt Im Koordinatenursprung.  im Wendepunkt W=(1|-1) ist die Tangente parallel zur ersten Achse. Ermittler eine Termdarstellung der Funktion f.

Könnte bitte jemand die 5 Bedingungen aufstellen?

Answer 1

Bedingungen

f(0)=0
f'(0)=0
f(1)=-1
f''(1)=0
f'(1)=0

Gleichungssystem

e = 0
d = 0
a + b + c + d + e = -1
12a + 6b + 2c = 0
4a + 3b + 2c + d = 0

Funktion

f(x) = -3·x^4 + 8·x^3 - 6·x^2

Für andere Aufgaben: http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

Comments

Kannst du mir erklären, wie du auf die Bedingungen kommst?

---

Der Graf eine Polynomfunktion f von Grad 4 hat einen hochpunkt Im Koordinatenursprung.

Die Funktion geht durch den Ursprung also durch den Punkt (0|0) → f(0) = 0

Im Ursprung hat man einen Hochpunkt. Notwendige Bedingung für Hochpunkte ist das die erste Ableitung Null ist. → f(0) = 0

im Wendepunkt W=(1|-1) ist die Tangente parallel zur ersten Achse.

Die Funktion geht durch den Punkt (1|-1). → f(1) = -1

Da es ein Wendepunkt ist muss die notwendige Bedingung, dass die zweite Ableitung Null wird, erfüllt sein. → f''(1) = 0

Und da die Tangente parallel zur x-Achse ist hat sie die Steigung 0 und damit muss der Graph auch die Steigung von 0 haben. → f'(1) = 0

---

Vielen lieben Dank! Ich wünschte mein Mathelehrer könnte auch so verständlich erklären!

---

Warum muss f''(1) = -1 sein?

---

@Spacko

Richtig. Es müsste wie oben in meiner Antwort natürlich f''(1) = 0 lauten.

War nur ein Test ob Susi auch aufpasst.

---

Hallo coach,
Da es ein Wendepunkt ist muss die notwendige Bedingung, dass die zweite Ableitung Null wird, erfüllt sein. → f''(1) = -1

Oben hast du es richtig geschrieben
f''(1) = 0

Ein klitzkleines Fehlerchen welches keinen
weiteren Einfluß auf das Weltgeschehen hat.

---

... stimmt nun f‘‘(1)=-1 oder f“(1)=0

---

f “ (1)=0
Eine Krümmung an einem Wendepunkt hat den Wert 0.
Sollte man wissen.

---

Richtig. Es müsste wie oben in meiner Antwort natürlich f''(1) = 0 lauten.

 Da es ein Wendepunkt ist muss die notwendige Bedingung, dass die zweite Ableitung Null wird, erfüllt sein. → f''(1) = 0

Answer 2

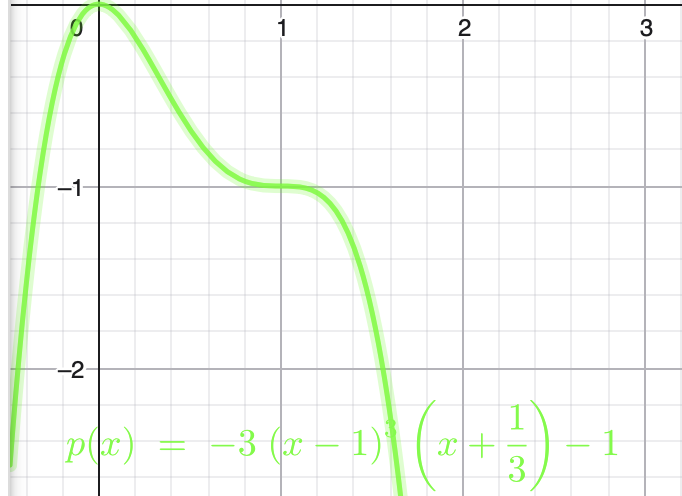
Der Graf eine Polynomfunktion f von Grad 4 hat einen Hochpunkt Im Koordinatenursprung.  Im Wendepunkt W=(1|-1) ist die Tangente parallel zur ersten Achse. Ermittle eine Termdarstellung der Funktion f.

Ich verschiebe den Graph um 1 Einheit nach oben   W=(1|-1)→  W=(1|0)

Der Graph hat im Wendepunkt eine dreifache Nullstelle.

Linearfaktorenform:

\( f(x)= a(x-1)^3(x-N)    \) 

...hat einen Hochpunkt Im Koordinatenursprung.  H(0I0) →  H´(0I1)   1. Ableitung :

\( f'(x)= a[3(x-1)^2(x-N)+(x-1)^3 ]   \)

\( f'(0)= a[3(0-1)^2(0-N)+(0-1)^3 ] =a[-3N-1]=0 \)

\(N=-\frac{1}{3} \)

\( f(x)= a(x-1)^3(x+\frac{1}{3})    \)

H´(0I1):

\( f(0)= a(0-1)^3(0+\frac{1}{3}) =-\frac{1}{3}a =1  \)

\( f(0)= a(0-1)^3(0+\frac{1}{3}) =-\frac{1}{3}a =1  \)

\( a=-3  \)

\( f(x)= -3(x-1)^3(x+\frac{1}{3})    \)

Nun um eine Einheit nach unten verschieben:

\( p(x)= -3(x-1)^3(x+\frac{1}{3})-1    \)