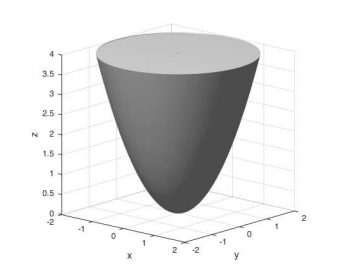
Für \( s \in[0,2], r \in[0,1], \varphi \in[0,2 \pi] \) sei ein Körper K durch diese Parametrisierung gegeben:
\( \Phi(s, r, \varphi)=\left(\begin{array}{c}s r \cos \varphi \\ s r \sin \varphi \\ s^{2}\end{array}\right) \)
Außerdem sei für a ∈ ℝ ein Vektorfeld gegeben durch:
\( w(x, y, z)=\left(\begin{array}{c}1 \\ 2 y \\ 3 x^{2} z\end{array}\right) \)
a) Berechnen Sie den Fluss des Vektorfelds \( w \) durch die Oberfläche des Körpers \( K \) direkt,
d. \( h \). durch Oberflächenintegrale.
b) Lösen Sie die Aufgabe über ein Volumenintegral mit dem Satz von Gauß.
Meine Lösungen:
Parametrisierung für Boden mit \( s \in[0,2], \varphi \in[0,2 \pi] \)
$$ \begin{array}{c} \Phi(s, \varphi)=\left(\begin{array}{c} s \cos \varphi \\ s \sin \varphi \\ s^{2} \end{array}\right) \Rightarrow w(\Phi(s, \varphi))=\left(\begin{array}{c} 1 \\ 2 s \sin \varphi \\ 3 s^{4} \cos ^{2} \varphi \end{array}\right) \\ n(s, \varphi)=\Phi_{\varphi}(s, \varphi) \times \Phi_{s}(s, \varphi)=\left(\begin{array}{c} -s \sin \varphi \\ s \cos \varphi \\ 0 \end{array}\right) \times\left(\begin{array}{c} \cos \varphi \\ \sin \varphi \\ 2 s \end{array}\right)=\left(\begin{array}{c} 2 s^{2} \cos \varphi \\ 2 s^{2} \sin \varphi \\ -s \end{array}\right) \end{array} $$
Wie komme ich oben auf Φ(s,φ) =( )
Was wurde da gemacht, welche Rechenoperation?
Gruß
