Question

Beschreiben und beurteilen Sie die gezeigte Beweisführung eines Schülers zur folgenden Aussage: , per Mittelpunktswinkel ist doppelt so groß wie der Peripheriewinkel".

Kann mir jemand erklären, wo die Fehlerquellen liegen?

Answer 1

Hallo

an dem Beweis ist so nichts falsch, aber wenn man noch nicht hat, dass alle Winkel über einer Sehne gleich groß sind, gilt der Beweis nur für die Spezielle Lage des Dreiecks.(also gleichschenkliges Sehnendreieck)

Gruß lul

Answer 2

Die Skizze zeigt einen Spezialfall. So wäre sie allgemeiner:

Dazu der Beweis von Mathecoach (Kommentar unten).

Comments

α + β + γ = 360°

β + 2·ε = 180° --> β = 180° - 2·ε

γ + 2·δ = 180° --> γ = 180° - 2·δ

II und III in I einsetzen

α + 180° - 2·ε + 180° - 2·δ = 360°

α - 2·ε - 2·δ = 0

α = 2·ε + 2·δ

α = 2·(ε + δ)

---

In der Elementargeometrie dieses Niveaus sind negative Winkel nicht üblich.

---

Natürlich wäre es schöner, einen elementargeometrischen Beweis zu haben, der mit weniger Algebra auskommt, so wie dieser:

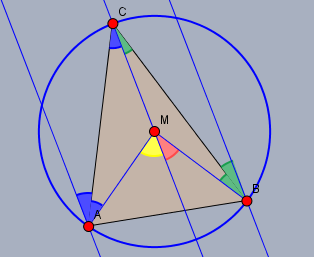
aber der wesentliche Fehler besteht - wie schon erwähnt - darin, dass nur der Spezialfall bewiesen wurde, bei dem der Punkt \(C\) auf der Mittelsenkrechten von \(AB\) liegt.

---

man könnte vielleicht noch bemängeln, dass zu wenig die Vorausetzungen beschrieben wurden. Zum Beispiel: $$|MA| = |MC| \implies \triangle AMC \text{ gleichschenklig} \\ \implies \angle MAC = \angle ACM$$usw.

---

So ist es besser.

Was ich meinte ist, dass MCs Rechnung isofern immer noch zu speziell ist als in dieser Lage der Punkte

andere Winkel oder negative Winkelgrößen erforderlich sind.