Determinante einer Matrix mit komplexen Zahlen berechnen

Question

Aufgabe:

Text erkannt:

Da es sich bei \( A \) um eine \( 2 \times 2 \) -Matrix handelt ist \( \operatorname{det}(A)=(1-i) \cdot(-14+2 i)-2 i \cdot(2-i)= \) \( -14+12 i \mathrm{mit}|\operatorname{det}(A)|^{2}=14^{2}+12^{2}=340 \) und weiter die Inverse zu \( A \) gegeben durch

Problem/Ansatz:

Ich habe die Determinante berechnet von der 2x2-Matrix mit komplexen Zahlen: -14 + 12i, wieso macht man jetzt noch den Betrag und dazu noch wie Wurzel? Damit das i verschwindet? Der Beträg wäre ja 14+12i, wieso darf man einfach a und bi einzeln quadrieren?

Und wieso rechnen wir danach nicht einfach 1/det(A) * A, sondern so:

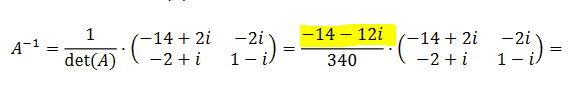
Text erkannt:

\( A^{-1}=\frac{1}{\operatorname{det}(A)} \cdot\left(\begin{array}{cc}-14+2 i & -2 i \\ -2+i & 1-i\end{array}\right)=\frac{-14-12 i}{340} \cdot\left(\begin{array}{cc}-14+2 i & -2 i \\ -2+i & 1-i\end{array}\right)= \)

??

Answer 1

Also die inverse einer 2x2 Matrix ist nicht $$  A^{-1} \ne \frac{1}{\det{A}} \cdot A $$ sondern $$ A^{-1} = \frac{1}{\det{A}} \cdot \text{adj}A $$  und ob man den Nenner reell macht oder nicht ist eine Geschmacksfrage.

Comments

also ja, ich meinte die Adjunkte mit

d -b

-c a

Ich verstehe nicht genau, wieso man das mit dem Betrag macht.

---

Geschmacksfrage. Den Nenner reell machen. Sonst ist da nichts.

---

Hallo,

ich möchte noch auf Folgendes hinweisen: "Der Beträg wäre ja 14+12i,." Das ist falsch, bitte schlage die Definition des Betrags einer komplexen Zahl nach.

Gruß