Bestimmen sie die Koordinaten des Punktes P so, dass der Flächeninhalt maximal wird und berechnen sie diesen.

Question

Aufgabe:

Siehe Bild.

Text erkannt:

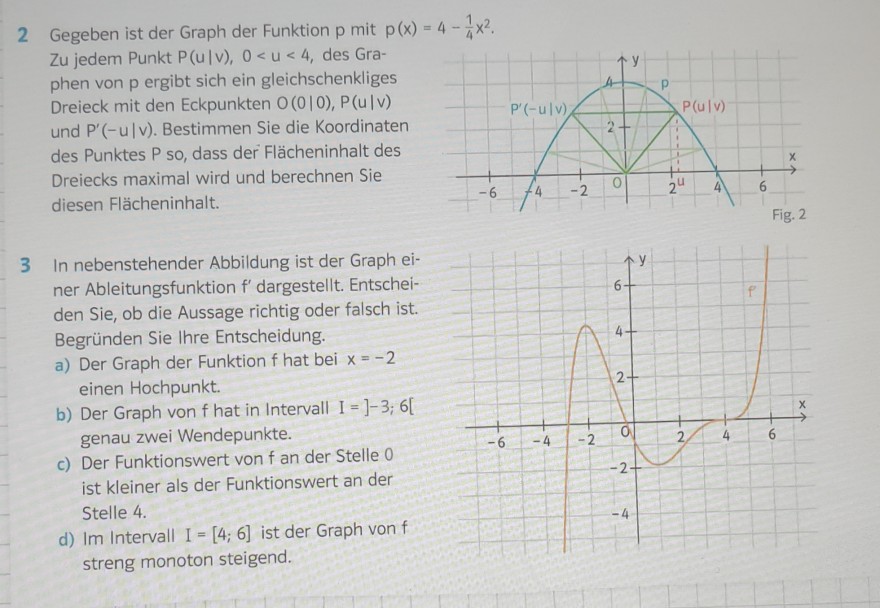
2 Gegeben ist der Graph der Funktion \( \mathrm{p} \) mit \( \mathrm{p}(\mathrm{x})=4-\frac{1}{4} \mathrm{x}^{2} \) Zu jedem Punkt \( \mathrm{P}(\mathrm{u} \mid \mathrm{v}), 0<\mathrm{u}<4, \) des Graphen von p ergibt sich ein gleichschenkliges Dreieck mit den Eckpunkten \( 0(0 \mid 0), P(u \mid v) \) und \( \mathrm{P}^{\prime}(-\mathrm{u} \mid \mathrm{v}) \). Bestimmen Sie die Koordinaten des Punktes \( \mathrm{P} \) so, dass der Flächeninhalt des Dreiecks maximal wird und berechnen Sie diesen Flächeninhalt.
3 In nebenstehender Abbildung ist der Graph einer Ableitungsfunktion f' dargestellt. Entscheiden Sie, ob die Aussage richtig oder falsch ist. Begründen Sie Ihre Entscheidung.
a) Der Graph der Funktion \( f \) hat bei \( x=-2 \) einen Hochpunkt.
b) Der Graph von \( f \) hat in Intervall \( I=]-3 ; [6 \) genau zwei Wendepunkte.
c) Der Funktionswert von \( f \) an der Stelle 0 ist kleiner als der Funktionswert an der
Stelle \( 4 . \)
d) \( \mid m \) Intervall \( I=[4 ; 6] \) ist der Graph von \( f \) streng monoton steigend.

Problem: Bei Nr 2. Habe ich keine Idee noch einen Ansatz wie ich diese lösen soll. Für die Nr. 3 bräuchte ich nur Hilfe bei der Funktiongleichung des Graphen.

Answer 1

Text erkannt:

\( p(x)=4-\frac{1}{4} x^{2} \)
\( p(u)=4-\frac{1}{4} u^{2} \)
\( A(u)=2 u \cdot \frac{p(u)}{2} \)
\( A(u)=2 u \cdot \frac{4-\frac{1}{4} u^{2}}{2} \) soll maximal werden
\( A(u)=u \cdot\left(4-\frac{1}{4} u^{2}\right)=4 u-\frac{1}{4} u^{3} \)
\( \mathrm{A}^{\cdot}(u)=4-\frac{3}{4} u^{2} \)
\( 4-\frac{3}{4} u^{2}=0 \)
\( \frac{3}{4} u^{2}=4 \)
\( u^{2}=\frac{16}{3} \)
\( u=\frac{4}{\sqrt{3}} \rightarrow \rightarrow p(u)=4-\frac{1}{4} \cdot \frac{16}{3}=4-\frac{4}{3}=\frac{8}{3} \)
\( A\left(\frac{4}{\sqrt{3}}\right)=\frac{4}{\sqrt{3}} \cdot \frac{8}{3}=\frac{32}{3 \cdot \sqrt{3}} \approx 6,16 \)

Comments

Vielen Dank!! Könnten Sie mir evtl. noch mit der Aufgabe 3 weiterhelfen?

---

Wie berechne ich die Koordinaten des Punktes P?

---

Wie berechne ich die Koordinaten des Punktes P?

x=\( \frac{4}{3} \)*3^(\( \frac{1}{2} \) )  in f(x)=4-\( \frac{1}{4} \) x^2  einsetzen.

Answer 2

2. Flächeninhalt des Dreiecks u·v=u·(4-u²/4); also F(u)=4u-u³/4.

Nullstellen der ersten Ableitung von F auf Maximum untersuchen.