Wie berechnet man bei diesem Dreieck (39/30/39) den Umkreis und den Inkreis?

Question

Ein dreieck hat folgende seitenlängen: 39/30/39. Berechne den Inkreis- und Umkreismittelpunkt unter verwendung eines rechtwinkligen teildreiecks? Wie sollte ich da vorgehen?

Comments

Hier musst du den Schnittpunkt der Mittelsenkrechten resp. der Winkelhalbierenden berechnen.

Du kannst das Dreieck, das übrigens gleichschenklig ist, in ein Koordinatensystem einzeichnen und dann mit Geradengleichungen arbeiten. Z.B. Basis mit Länge 30 auf der x-Achse.

Gibt leider keine 'schönen' Zahlen. Speichere die Zwischenresultate am besten ab.

---

Es gibt ganz schöne Zahlen.... Zum ersten ist es ein pythagoreisches Trippel und zweitens wurden die Zahlen so gewählt, dass es eine einfache Lösung herauskommt.....

Answer 1

Diese Aufgabe hatte ich auch... Arbeitest du mit dem Buch Algebra 1? :-)

Zum Lösen der Aufgabe: Der Inkreis kann man mit der Formel ρ(Symbol für den Inkreis)=A(Fläche des Dreiecks)/s(der halbe Umfang). Jetzt musst du nur noch deine Werte eingeben und du hast die Lösung für den Inkreis:

h=√(39²-15²)=36  ⁽¹⁾

A=0.5*c*h=15*36=540

s=(39+39+30)/2=39+15=54

ρ=A/s=10

 

Zum Umkreisradius:

Dieser ist ein wenig schwieriger zu berechnen, darum zuerst eine Grafik:

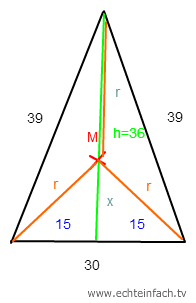
Wie du siehst, habe ich x schon definiert, was auf eine Gleichung kommt....

Zuerst mal das Wichtigste zusammenfassen:

r²=15²+x²;

r=36-x

Und nun die Gleichung:

(36-x)²=225+x²

1296-72x+x²=225+x²

1071=72x

14.875=x

 

Dementsprechend ist r=36-14.875=21.125

 

Dies ist schon alles was du tun musst......

 

Ich hoffe, du verstehst es nun und ich konnte dir helfen!

Simon

 

⁽¹⁾Dies ist ein Pythagoreisches Tripel

Comments

Ist es nicht so : für den Umkreismittel den schnittpunkt der drei Mittelsenkrechten braucht, und für den Inkreis den Schnittpunkt der winkelhalbierenden?

---

Eigentlich schon. Nur kennt simonai offenbar eine Formel für den Inkreisradius. Da das Dreieck noch gar nicht in einem Koordinatensystem vorliegt und symmetrisch ist, kann er auch nach der Berechnung der Radien noch die Koordinaten der Mittelpunkte ausrechnen.

---

Ich habe diese Aufgabe im Unterricht mit dem Lehrer gelöst, desshalb kenne ich den Lösungsweg und die Lösung...