lim x->2 (-2x3+8x2)/(x2-4x+4)

Question

Aufgabe:

lim x->2   (-2x³+8x²)/(x²-4x+4)

x >2 und x<2

Problem/Ansatz:

Warum ist das Ergebnis für beiden -∞.

meine Ergebnis ist für beide 16 (∞)= +∞

Answer 1

Aloha :)

$$\frac{-2x^3+8x^2}{x^2-4x+4}=-\frac{2x^2(x-4)}{(x-2)^2}$$Der Zähler ist für $x<4$ immer negativ. Der Nenner ist als Quadratzahl nie negativ. Wegen dem Minuszeichen vor dem Bruch, ist der Bruch also für $x<4$ positiv. Der Grenzwert für $x\to2$ ist also von beiden Seiten her $+\infty$.

Plotlux öffnen

f₁(x) = (-2x³+8x²)/(x²-4x+4)Zoom: x(0…5) y(-10…200)

Comments

im Ergebnis steht -∞ und nicht +∞

---

Das Soll-Ergebnis ist ja auch falsch... Dein Ergebnis ist richtig.

---

Frage dazu, kann man in diesem Fall nicht auch l´Hospital anwenden ?

---

Nein. Dann müsste der Ausdruck gegen "0/0" streben, aber der Zähler

macht da nicht mit!

---

ah das habe ich übersehen, danke

Answer 2

Der Ausdruck ist gleich $\frac{-2x^2(x-4)}{(x-2)^2}$.

Der Zähler ist in der Nähe von $2$ positiiv und der Nenner ist als

Quadrat immer $\geq 0$. Also ist der Limes $=\infty$.

Überschneidung mit Tschakabumba :-)

Answer 3

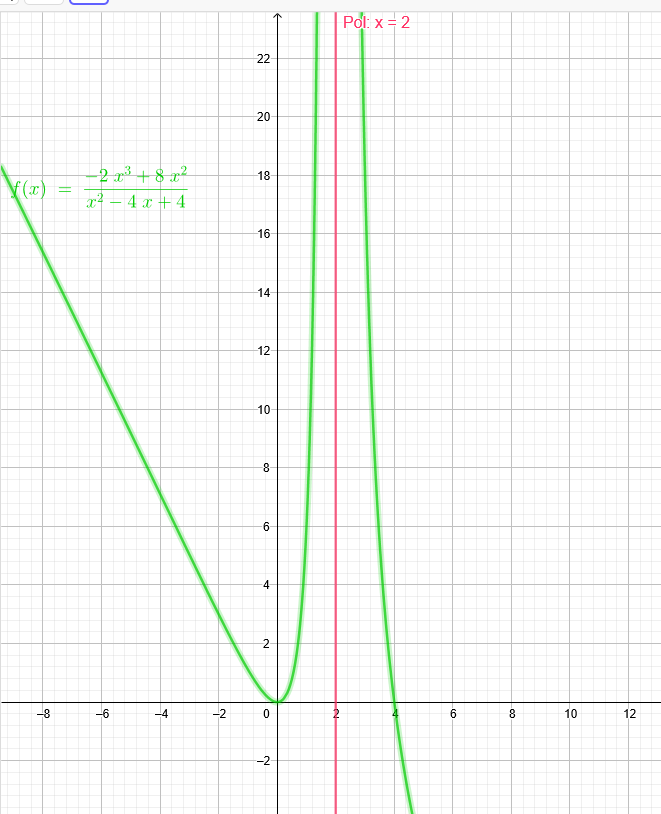
f(x)=$\frac{-2x^3+8x^2}{x^2-4x+4}$=$\frac{-2x^3+8x^2}{(x-2)^2}$

Wenn du nun den Nenner =0 setzt, bekommst du als Lösung x=2

Bei x=2 existiert ein Pol.

x<2       f(1.9)=$\frac{-2*(1,9)^3+8*(1,9)^2}{(1,9-2)^2}$=1516,2

x>2      f(2,1)=$\frac{-2*(2,1)^3+8*(2,1)^2}{(2,1-2)^2}$=1675,8

Je mehr du dich der 2 näherst, siehst du, dass der Grenzwert von beiden Seiten her +∞ ist.