Hallo,
3 bitte machen diese ist schwierigste
Die Flächen des Trapez' und des Dreiecks sind gleich groß. Um dies zu zeigen, zerlege beide Fguren in 6 identische rechtwinklige Dreiecke. Für die Hälfte der Dreiecke habe ich es Dir hier skizziert:
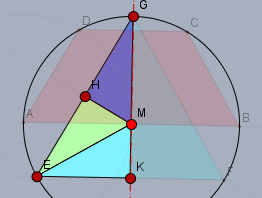

jedes der rechtwinkligen Dreiecke hat die Hypotenuse der Länge \(r=|AM|\) und die kleinere Kathete hat die Länge \(r/2\). Die Innenwinkel sind \(30°\), \(60°\) und \(90°\).
Tipp: das Dreieck \(\triangle AMD\) ist ein gleichseitiges.
Nachtrag:
ich verstehe wirklich nichts
.. ist auch 'ne schöne Ausrede; so musst Du auch nichts tun. Und bei dieser Aufgabe kannst Du was tun!
Nimm ein Blatt Papier, Bleistift, Lineal und Zirkel. Und dann zeichne eine waagerecht liegende Gerade und darauf einen Kreis, so dass der Mittelpunkt \(M\) des Kreises auf dieser Geraden liegt. Der Kreis schneidet die Gerade in den Punkten \(A\) und \(B\). Und dann mit dem gleichen Radius nochmal zwei Kreise mit den Mittelpunkten \(A\) und \(B\). Das sieht so aus:

die beiden letzten Kreise schneiden den ersten in den Punkten \(D\) und \(C\) (oberhalb der blauen Geraden).
Damit ist Dein Trapez \(ABCD\) fertig und es besteht aus lauter gleich langen Strecken.
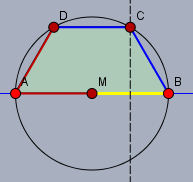
Jede der roten, blauen und gelben Strecke ist gleich lang. Nun nimm noch eine Schere, schneide das Trapez aus und anschließend schneide vom Trapez noch die Ecke bei \(B\) ab. Der Schnitt muss durch \(C\) und senkrecht zur Basis \(AB\) erfolgen.
Die abgeschnittene Ecke setzt Du unten wieder an:
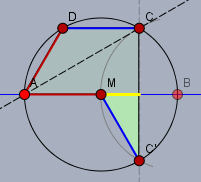
Jetzt schneidest Du nochmal entlang der Geraden \(AC\) ein Dreieck ab. Und dieses Dreieck legst Du in die Lücke bei \(M\):
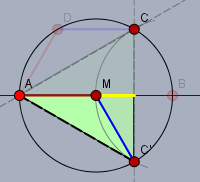
und so entsteht das gleichseitige Dreieck \(AC'C\), was genau in den Kreis passt. Damit hast Du gezeigt, dass beide Figuren gleich groß sind.
.. bitte ich verstehe nix.
Dann solltest Du etwas tun und Dich nicht faul und bequem auf 'nix verstehn' zurück ziehen! Mathematik ist mehr ein TUN und ein DENKEN.
Wäre übrigens nett, wenn Du Dich zu dem Thema nochmal meldest.