Gib das Längenverhältnis der Radien an

Question

Zwei gleichgroße Kreise mit dem Radius t, die sich berühren und ein dritter Kreis mit dem Radius t/2,der die beiden ersten Kreise berührt, liegen in einem größeren Kreis mit dem Radius r, den jeder von ihnen berührt . Gib t in Abhängigkeit von r an.

Comments

Ich würde ein gleichseitiges Dreieck einzeichnen, dass aus Radien der Innenkreise besteht.

Stimmt dieser Ansatz?

---

Das ist nur der Anfang eines Ansatzes.

---

Hallo Roland,

Habe alle drei innen liegenden Kreise den Radius \(r\), dann ist zu leicht!$$\frac tr = 2\sqrt 3\,-3$$(im Kopf ausgerechnet)

---

Vielleicht protokollierst du kurz deinen Gedankengang? Ich habe etwas anderes heraus.

---

Du hattest diese Frage schon mal gestellt. Inzwischen habe ich sie auch gefunden.

https://www.mathelounge.de/590055/drei-kreise-in-einem-grosseren-kreis

mathef hat dort das identische Ergebnis.

---

siehe auch http://www.mathematische-basteleien.de/kreise_im_kreis.htm

---

Ja, ich muss mich für meine Frage entschuldigen. Ich ziehe sie zurück.

---

Wandel sie doch um. Einer der drei Kreise ist kleiner und hat den Radius \(t_2\). Das Verhältnis von \(t\div t_2\) sei gegeben.

Und als Goodie: konstruiere die Figur mit Zirkel und Lineal.

---

Zum Thema ‚Kreise im Kreis‘ kann ich dies wärmstes empfehlen:

https://m.youtube.com/watch?v=sG_6nlMZ8f4

---

@ Werner: Vielen Dank. Aufgabe geändert.

---

Das war wohl nichts.

Richtig ist   r = t*(2+√5)/2

---

Und als Goodie: konstruiere die Figur mit Zirkel und Lineal.

Wieder ein typischer Werner.

Könnte etwa folgendermaßen gehen :

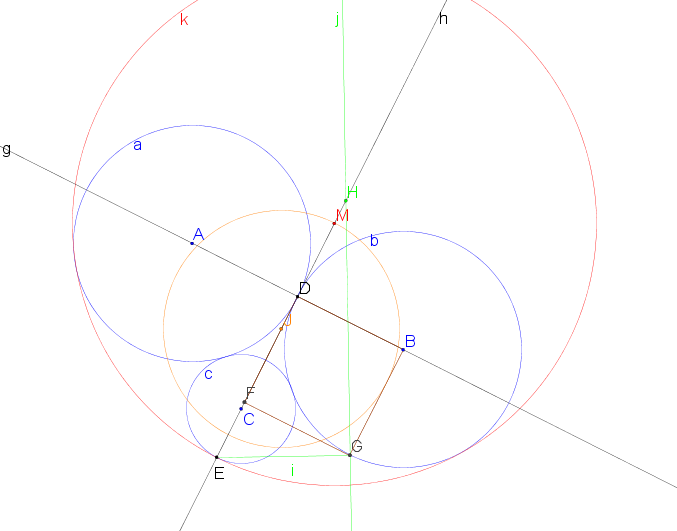
Gegeben sind Kreise a,b,c um A,B,C mit Radien r_a=r_b=r und r_c . (blau)

1. Man zeichne den Berührpunkt D sowie die Geraden g durch A und B und h durch C und D sowie den Schnittpunkt E von h mit c. (schwarz)

2. Man zeichne das Quadrat BDFG. (braun)

3. Man zeichne die Strecke i = EG und die Gerade j senkrecht zu i durch G, Schnittpunkt mit h ist H. (grün)

4. Man zeichne den Mittelpunkt J zwischen E und H und den Kreis um J mit Radius r. (orange)

5. Man zeichne den Schnittpunkt M dieses Kreises mit h und den gesuchten Kreis k um M durch E. (rot)

Und da du einen Link bereitgestellt hast, kommt hier auch noch einer von mir :
http://jwilson.coe.uga.edu/EMAT6680Su09/Floer/6690/Soddy%20Circles/Soddy%20Circles.html

---

@hj2166

Werners Antwort, die du als falsch benennst, bezog sich auf eine Frage, die ich auf Werners Rat später verändert hatte.

---

Mein Kommentar bezog sich auf einen Unsinn, den döschwo verzapft hatte und den er aufgrund meines Beitrags kommentarlos gelöscht hat. Wahrscheinlich wird er das wieder einem ominösen Eierdieb in die Schuhe schieben.

---

Ist halt verwirrlich, wenn die Aufgabe geändert wird. Und nein, denn der Eierdieb klaut keinen Unsinn. Ich bin auch weder Schuheschieber noch Schuheschieberin. Aber ominös ist er, ja. Und Du solltest mal über Deinen Benutzernamen nachdenken, so ganz legal ist das nicht.

---

@hj: interessante Konstruktion. Sie riecht ein wenig danach, dass Du es zuerst analytisch berechnet hast und dann erst die Lösung in die Konstruktion gegossen hast.

Hier eine Alternative, die im Grunde ganz ähnlich ist:

Zwei Kreise mit Mittelpunkt \(A\) und \(B\) und Radius \(r_a=r_b=t\) berühren sich in \(D\). Ein dritter Kreis \(k_c\) mit Mittelpunkt \(C\) und Radius \(r_c\) berührt beide Kreise.

Die Gerade durch \(CD\) schneidet \(k_c\) auf der der Geraden durch \(AB\) abgewandten Seite in \(E\). Der Kreis um \(E\) mit Radius \(t\) (orange) schneidet die Gerade durch \(CD\) auf der der Geraden durch \(AB\) zugewandten Seite in \(F\).

Man konstruiere den Mittelpunkt \(M\) des Umkreises des Dreiecks \(\triangle AFB\). Der Kreis um \(M\) mit Radius \(|ME|=r\) (rot) ist der gesuchte äußere Kreis.

---

Mit den zusätzlichen Strecken, die ich in die Skizze meines vorhergehenden Kommentars eingezeichnet habe, sollte es doch ein Leichtes sein, das Verhältnis \(t/r\) für \(r_c=t/2\) zu berechnen.

Freiwilllige vor ;-)