Hallo kolt,
wie Roland schon erwähnt hat, genügt es nicht zu zeigen, dass die Anzahl der Felder minus 1 durch 3 teilbar ist. Nehme z.B. mal ein Feld von \(3\times 3\). Es besteht aus 9 Feldern. Und man kann es trotzdem nicht vollständig mit 3 L-förmigen Puzzlestücken auslegen. Versuche es einfach mal.
Beginne mit dem Induktionsanfang. Für \(n=1\) sieht das Feld so aus:
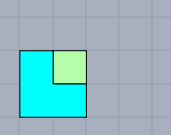
Es ist ein \(2\times 2\)-Feld und das freie Feld liegt in diesem Fall immer in einer Ecke. Und in den Rest passt das L-Stück genau hinein. Damit ist für \(n=1\) gezeigt, dass es geht.
.. und wir kommen zum Induktionsschritt:
Es ist zu zeigen, dass man ein Feld von \(2^{n+1} \times 2^{n+1}\) so mit den L-Stücken auslegen kann, dass ein beliebiges Feld frei bleibt. Wir dürfen dazu annehmen, dass es bei einem \(2^n\times 2^n\)-Feld möglich ist (das ist die Induktionsannahme). Das neue Feld ist viermal so groß, jede Kantenlänge hat sich verdoppelt. D.h. es liegt nahe, es in vier gleich große Quadrate zu zerteilen:
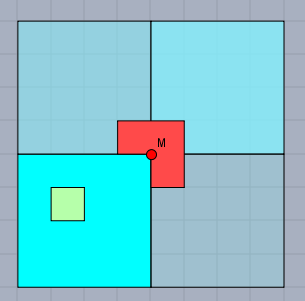
Das Quadrat links unten ist ein \(2^n\times 2^n\)-Feld und enthält bereits das freie Feld (grün). Die anderen drei Teilquadrate legen wir nun so mit L-Stücken aus, dass das freie Feld jedes der drei zusätzlichen Teilquadrate den Mittelpunkt \(M\) berührt. Dies ist ja möglich, da diese ebenfalls \(2^n\times 2^n\)-Felder sind (s. Induktionsannahme). Und in die so entstandene freie Stelle passt wieder genau ein L-Stück hinein (rot).
Und da man das ganze Gebilde jeweils um 90° drehen kann und vorher das grüne Feld beliebig plazieren kann, kann das freie Feld sich an jeder beliebigen Stelle befinden.
Damit ist bewiesen, dass es auch für \(2^{n+1}\times 2^{n+1}\)-Felder möglich ist.
Gruß Werner