Bestimme einen von P verschiedenen Punkt Q auf dem Graphen der Funktion f, in dem die Tangente parallel zur Tangente …

Question

Aufgabe:

Bestimme einen von P verschiedenen Punkt Q auf dem Graphen der Funktion f, in dem die Tangente parallel zur Tangente im Punkt P ist!

f(x)= x³, P=(1/ f(1))

Answer 1

Welchen Anstieg hat die Tangente im Punkt P?

An welcher Stelle des Graphen von f ist die Ableitung  genau so groß ist?

Comments

Hallo Abakus,

Ich bin auf 3 gekommen (Steigung der Tangente=erste Ableitung der Funktion) (eigene Berechnungen).

Ist das richtig?

Lg Bono Bo

---

Ja,

An welcher Stelle (außer x=1) gilt auch noch f'(x)=3?

---

Hallo,

Wenn man mit der Ableitung weiterrechnet ist auch -1 möglich oder?

Lg

Answer 2

Tangente in $P$ ist $$t_1(x) = 3(x-1)+1$$ und Tangente in $Q$ ist $$t_2(x) = 3 ( x+1) -1$$

Was ist $Q$?

Comments

Hallo Ullim,

Vielen Dank für die schnelle Beantwortung meiner Frage!

Ich verstehe dennoch nicht, wie man auf Tangentengleichungen in den Punkten P und Q kommt, ich dachte dass das einfach die erste Ableitung der Funktion sei..?

Besten Dank

Bono Bo

---

Die Tangentengleichung an eine beliebige Funktion $f(x)$ im Punkt $(x_0 , f(x_0) )$ lautet

$$t(x) = f'(x) (x-x_0) + f(x_0)$$

Die erste Tangente geht durch $(1 , f(1) )$

Da $f'(8) = 3 x^2$ gilt, ist die Steigung in obigem Punkt $3$, aber eben auch, wie Du selber bemerkst hats auch für $x_1 = -1$

Kommst Du damit weiter?

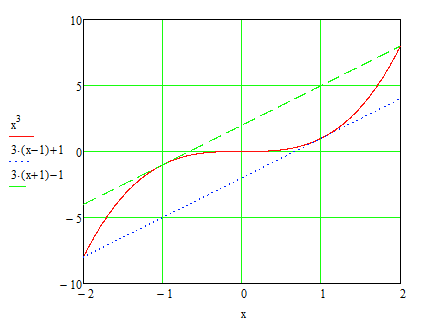
Aussehen tut es so