Eine 18 m hohe Tanne soll gefallt werden. In welcher Entfernung vom Stammende schlägt die Spitze auf dem Boden auf, wenn die Tanne 1,50 m über dem Boden geschlagen wird?
Planfigur:
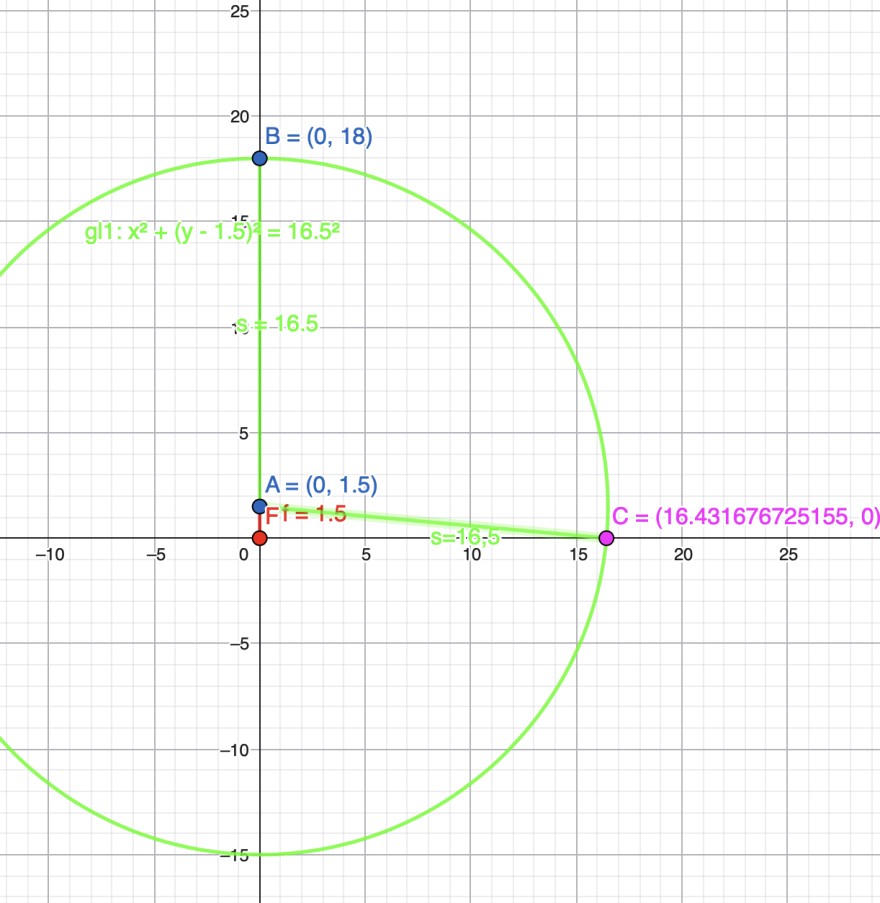
Allgemeine Kreisformel:
\( (x-x_M)^{2}+(y-y_M)^2=r^2\)
\( x_M=0\) \( y_M=1,5\) \( r=16,5\)
\( x^2+(y-1,5)^2=16,5^2\)
Nullstelle der Kreisgleichung:
\( x^2+(0-1,5)^2=16,5^2\)
\( x^2+2,25=272,25\)
\( x^2=270\)
\( x=\sqrt{270}≈16,43\)
Die Entfernung beträgt \( 16,43\) m