Question

Bestimmen Sie den Term einer ganzrationalen Funktion dritten Grades, deren Graph die
y-Achse bei - 2 schneidet und dort die Steigung 2 besitzt. Des Weiteren besitzt die gesuchte
Funktion den Hochpunkt H (2|4).

Ich habe leider gar keine Ahnung was sich hier machen Soll. Könnte mir jemand die Vorgänge erklären um zur Lösung zu kommen?

Vielen Dank :)

Answer 1

Hallo

du hast f(x)=ax^3+bx^2+cx+d du brauchst noch f'(x)

du weisst f(0)=-2, f'(0)=2

und f(2)=4 und f'(2)=0

das sind 4 Gleichungen für die 4 Unbekannten a,b,c,d

Gruß  lul

Comments

Danke! Aber was genau muss ich danach machen, also wie bekomme ich jetzt die Zahlen für die die unbekannten?

Und wie kommt man auf f’(2)=0?

---

Hallo

im Hochpunkt ist die Steigung 0 deshalb f'(2)=0

wenn du die 4 Bedingungen eingesetzt hast hast du 4 lineare Gleichungen, die musst du lösen.

die erste Bei myung gibt direkt d=-2

die zweite c=2

damit hast du nur noch 2 Gleichungen mit den 2 unbekannten a und b.

Gruß lul

Answer 2

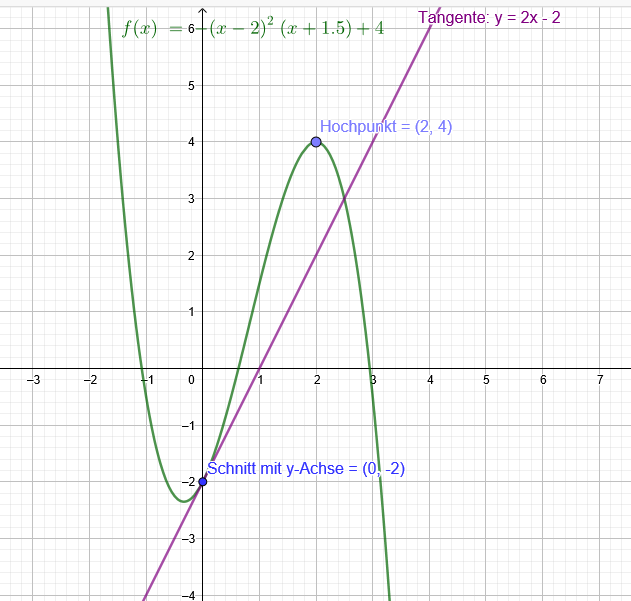
Bestimmen Sie den Term einer ganzrationalen Funktion dritten Grades, deren Graph die  y-Achse bei - 2 schneidet und dort die Steigung 2 besitzt. Des Weiteren besitzt die gesuchte Funktion den Hochpunkt H (2|4).

Ich verschiebe den Graph von f(x) um 4 Einheiten nach unten H´(2|0)

f(x)=a*(x-2)^2*(x-N)

P´(0|-2-4)   wegen Schnitt der y-Achse bei y=- 2     

P´(0|-6)

f(0)=a*(0-2)^2*(0-N)=-4*a*N

1.)  -4*a*N=-6      1.)  a=\( \frac{1,5}{N} \)

f(x)=\( \frac{1,5}{N} \)*[(x-2)^2*(x-N)]

f´(x)=\( \frac{1,5}{N} \)*[2*(x-2)*(x-N)+(x-2)^2*1]

Steigung in P´(0|...) : m=2

f´(0)=\( \frac{1,5}{N} \)*[2*(0-2)*(0-N)+(0-2)^2]

2.) \( \frac{1,5}{N} \)*[2*(0-2)*(0-N)+(0-2)^2]=2

N≈-1,5    a≈-1

f(x)=-1*(x-2)^2*(x+1,5)

Nun wieder 4 Einheiten nach oben:

p(x)=-(x-2)^2*(x+1,5)+4

Answer 3

Ich habe leider gar keine Ahnung

Das ist sicherlich nicht gut und daher wird der Ansatz $$f(x) = ax^3+bx^2+2x-2$$ mit den beiden Bedingungen $$f(2)=4$$ und $$f'(2)=0$$ dir vermutlich nicht weiterhelfen, dennoch soll er als eine von mehreren Möglichkeiten nicht unerwähnt bleiben.