Verkettung von g und f ist eine lineare Abbildung Beweis?

Question

Aufgabe:

Sind f : V → W und g : W → Z lineare Abbildungen, so ist auch die

Verkettung f ◦ g : V → Z (mit (f ◦ g)(v) = f(g(v))) eine lineare Abbildung.

Problem/Ansatz:

Kann das wer beweisen? Meine bisherigen Ansätze: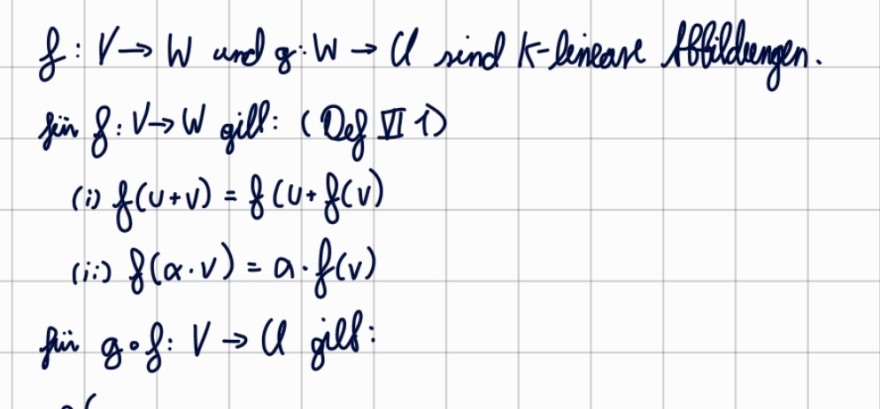

Text erkannt:

$f: V \rightarrow W$ und $g: W \rightarrow C$ sind $K$-leineare fffildengen. sin $f: V \rightarrow W$ gill: (Def II 1 )
(i) $f(u+v)=f(u+f(v)$
(ii) $f(\alpha \cdot v)=a \cdot f(v)$
fii $g \circ f: V \rightarrow$ gill:

Text erkannt:

Definition $4.12$ Seien $X, Y, Z$ Mengen und $f: X \rightarrow Y$ und $g: Y \rightarrow Z$ Abbildungen. Dann heißt die Abbildung
$\begin{aligned} g \circ f: X & \rightarrow Z \\ x & \mapsto g(f(x)) \end{aligned}$
die Verkettung von $f$ und $g$. Also gilt $(g \circ f)(x)=g(f(x))$.
Beispiel: Sei $f: \mathbb{R} \rightarrow \mathbb{R}_{0}^{+}, x \mapsto f(x)=x^{2}+1$ und $g: \mathbb{R}_{0}^{+} \rightarrow \mathbb{R}_{0}^{+}, x \mapsto g(x)=\sqrt{x}$. Daraus folgt, dass gilt:
$g \circ f: \mathbb{R} \rightarrow \mathbb{R}_{0}^{+},(g \circ f)(x)=\sqrt{x^{2}+1}$

Text erkannt:

Aufgabe 1 Beweisen Sie die Aussage aus Beispiel 6.3.(iv):
Sei $K$ ein Körper, seien $V, W, U K$-Vektorräume und seien $f: V \longrightarrow W, g: W \longrightarrow U$ $K$-lineare Abbildungen. Dann ist auch die Komposition $g \circ f: V \longrightarrow U$ eine $K$-lineare Abbildung.

Text erkannt:

Definific $\sqrt{\pi} 4$ falls fofentes gill:
(i) $f(u+v)=f(u)+f(v) \quad \forall u, v=V$
(ii) $f\left(\alpha_{\uparrow}, v\right)=\alpha_{v} f(v) \quad V_{v} \in V_{,}, \in t$

Text erkannt:

$V \times V \pm V$ ( geramt "Addition $\left.{ }^{\circ}\right)$
and
so dars folgendes gilf:
(i) $\left(V_{1}+\right)$ iss rine abliche Gmype
(ii) $\forall \alpha, \beta \in K$ und $a, b \in V$ gill
$\begin{array}{l} (\alpha+\beta) \cdot a=\alpha \cdot a+\beta \cdot a \\ a \cdot(a, b)=\alpha \cdot a+\alpha \cdot b \end{array}$
(i:i) $(\alpha \cdot \beta) \cdot a=\alpha_{i}(\beta \cdot a)$
mullink
shalare $\mu_{u}$ lf.
(iv) $I \cdot a=\alpha$ firi das Einebblmont $\mid \in K$ und $\forall_{a} \in V$.

Text erkannt:

$t i k \times k \rightarrow k$ (Addilition)
und $: i k x \rightarrow k($ Malijililation $)$ no dass $\forall a, b, c \in k$ folgendes gill:
(i) $(a+b)+c=a+(b+c)$ (Arrovalivitish der Hodilioin)
(ii) $\exists 0 \in K$ mit $0+a=a=a+0$ (newhales clement de toldinia)
(iii) $\forall a \in k \exists b \in k$ mit $a+b=0=b+a$ ( moese fientdoblifion)
(iv) $a+b=b+a$ (conmunilatiiitit der Aoldifion)
(v) $(a \cdot b) \cdot c=a \cdot(b \cdot c)$ (Kseoiativitial der Mullip)
(vi) $\exists 1 \in k$ mil $1 \cdot a=a=a \cdot 1$ (nucurales clement fin Multi)
(Vii) $\forall a \in \underbrace{k-\{0\}}_{k^{*}} \exists b \in k$ mit $b \cdot a=1=a \cdot b$ (hevers fin $\mu u l$ lij)
(viii) $a \cdot b=b \cdot a$ ( Kommm. dar. luad) )
(ix) $a \cdot(b+c)=a \cdot c+b \cdot c$ und $(a+b) c=a \cdot c+b \cdot c$ (Dihibakiogesta) $\}$
(x) $0 \neq 1$
Wir nemren dir Elemente Ound 1Nellelement und Einclelement oder harr Nall and Eins wan $k$.

Answer 1

Hallo

so wie du geschrieben hast geht das nicht:

f°g also f(g(w)) kann man nicht bilden denn g(w)=z z in Z und f bildet nicht Z ab. Steht da g geht von V->W? dann nur macht g(v) einen Sinn.
ich nehme mal an, das Z ist falsch.

dann schreib erst die vors hin : f(0)=0, f(r*v)=r*f(v) f(v1+v2)=f(v1)+f(v2) dasselbe für g mit w statt f.

jetzt f(g(0))=f(0)=0 erfüllt, f(g(r*w)=f(r*g(w))=r*f(g(w)) erfüllt  (du kannst zusätzlich g(w1)=v1 schreiben um es noch deutlicher zu machen.)

jetzt du mit f(g(w1+w2))=...

Also einfach nur die Linearität der inneren Funktion zuerst verwenden, dann die der äußeren

Gruß lul

Comments

Hallo lul, ich habe folgendes gemahct:

Text erkannt:

Aufgabe 1:
$z . z$.: Komposition gof: $V \rightarrow U$ ist linear.
Beweis
$\begin{aligned} (g \circ f)\left(\lambda v_{1}+\alpha v_{2}\right) &=g\left(f\left(\lambda v_{1}+\alpha v_{2}\right)\right) \\ &=g\left(\lambda \cdot f\left(v_{1}\right)+\alpha \cdot f\left(v_{2}\right)\right) \\ &=\lambda \cdot g\left(f\left(v_{1}\right)\right)+\alpha \cdot g\left(f\left(v_{2}\right)\right) \\ &=\lambda \cdot(g \circ f)\left(v_{1}\right)+\alpha \cdot(g \circ f)\left(v_{2}\right) \end{aligned}$

ist das richtig?

---

Ich habe die Def 6.1 genutzt

---

Das ist richtig, nur muss man schreiben wo bzw, dass man die Linearität von f  und von g benutzt.

du hast die 2 Eigenschaften die bei dir i und ii heißen zusammengefasst, das ist wohl ok, allerdings nicht so immer gemeint.

lul