Flächeninhalte von Flächen zwischen den Graphen zweier gegebener Funktionen

Question

Aufgabe:

Skizzieren sie den Graphen von f und g 7nd berechnen sie, wie groß der Flächeninhalt der von beiden Funktionsgraphen über dem Intervall I eingeschlossenen Flächen ist.

a) $f(x)=x^{3}-4 x+3 ; \quad g(x)=3 x-3 \quad I=[-3 ; 2]$

b) $f(x)=x^{2}-8 x+14 ; \quad g(x)=-x^{2}+6 x-6 \quad 1=[2 ; 5]$

c) $f(x)=-3 x^{2}+3 x+8 ; \quad g(x)=\frac{8}{x^{2}} \quad I=[1 ; 2]$

Problem/Ansatz:

Wie mache ich das?

Comments

Wie mache ich das?

So, wie Dir jemand am 11. Oktober 2022 geschrieben hat, nämlich:

Man könnte sich zunächst eine Skizze machen, damit man weiß was zu berechnen ist.

Das wird ja ausdrücklich auch im Aufgabentext verlangt. Bei der Aufgabe a) sieht die Skizze so aus:

---

Ich weiß aber nicht wie ich es ausrechnen soll? Können sie das am Beispiel von Aufgabe b) machen?

---

Man integriert die Differenzfunktion ("obere Kurve minus untere Kurve") vom linken bis zum rechten Schnittpunkt. Ich berechne als Beispiel den Inhalt der für Aufgabe a) skizzierten grünen Fläche:

$\begin{aligned} A &= \int\limits_{-3}^{1} (x^ 3-4x+3 - (3x-3)) \, dx &&+ \int\limits_{1}^{2} (3x-3-(x^ 3-4x+3)) \, dx \\\\ &= 32 &&+ 0,75 \end{aligned}$

Answer 1

Hier die ersten Schritte

Die Funktionen sind punktsymmetrisch
Schnittpunkte √7, - √ 7

Berechne die Stammfunktionen von f und g.
Berechne die Integrale ( getrennt ) von f und g zwischen
0 und √7 : ax,ay

A = abs(ax - ay ) * 2

A = abs(-49/4) * 2

Bei Bedarf nachfragen.

mfg

Comments

Korrektur
bei a.)
muß es für
g ( x ) = 3x minus 3
heißen

Ich kann das gerne nochmals richtig
berechnen.

Answer 2

Halo,

Aufgabe b)

1. Mache eine Skizze:

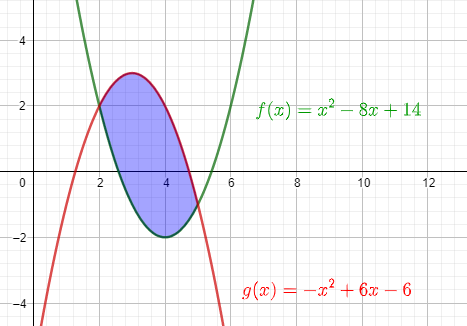
Bestimme die Schnittstellen der Funktionen, indem du sie gleichsetzt und nach x auflöst. Das sind die Integralgrenzen. Dabei erhältst du auch die Differenzfunktion h(x).

$x^2-8x+14=-x^2+6x-6\\\blue{2x^2-14x+20}=0\\x_1=2\quad x_2=5$

Bilde die Stammfunktion der Differenzfunktion.

$H(x)=\frac{2}{3}x^3-7x^2+20x$

Berechne das Integral $\int \limits_{2}^{5}(2x^2-14x+20)\;dx$, indem du den Betrag von H(5) - H(2) berechnest.

$\int \limits_{2}^{5}(2x^2-14x+20)\;dx=\bigg[\frac{2}{3}x^3-7x^2+20x\bigg]^5_2\\=\bigg|\red{\bigg(\frac{2}{3}\cdot 5^3-7\cdot 5^2+20\cdot 5\bigg)}-\green{\bigg(\frac{2}{3}\cdot 2^3-7\cdot 2^2+20\cdot 2\bigg)}\bigg|\\ =\bigg|\frac{25}{3}-\frac{52}{3}\bigg|=|-9|=9$

Gruß, Silvia

Comments

Hinweis: Die Fläche $F$ zwischen zwei Schnittpunkten bei $x_1=a$ und $x_2=b$  von Parabeln oder Parabel und Gerade kann man immer berechnen aus$$F = \frac 23(b-a)(f_o(m)-f_u(m)) \quad m= \frac{a+b}{2}$$Also in diesem konkretem Fall:$$F = \frac 23(5-2)\left(g\left(\frac72\right)-f\left(\frac 72\right)\right) \\ \phantom{F}= \frac 23 \cdot 3\left(\frac{11}{4} - \left(-\frac 74\right)\right) = 9$$