Löse die Gleichung rechnerisch und, wenn möglich, ohne Verwendung der Lösungsformel.

Question

G 18 Löse die Gleichung rechnerisch und, wenn möglich, ohne Verwendung der Lösungsformel.
a) $8 x-4=-3 x+4$
b) $5 x+5=3(x+2)$
c) $4 x=2 x(2 x+1)$
d) $3(2 x-5)=-(5-3 x)$
e) $10 x^{2}-5 x=2 x$
f) $7(x-4)+4=-3(-x-4)$
g) $\frac{1}{7} x^{2}-6=1$
h) $\frac{3}{8} x+\frac{3}{4}=\frac{1}{8}+x$
i) $\frac{1}{2} x-\frac{5}{6}=\frac{1}{2}\left(x-\frac{2}{3}\right)$
j) $4 x^{2}-4 x+1=0$
k) $4 x-3-x^{2}=3 x-9$
l) $x^{2}-2 x^{2}+46=67$

Comments

Wie heißt das Fach, dass du studierst?

Answer 1

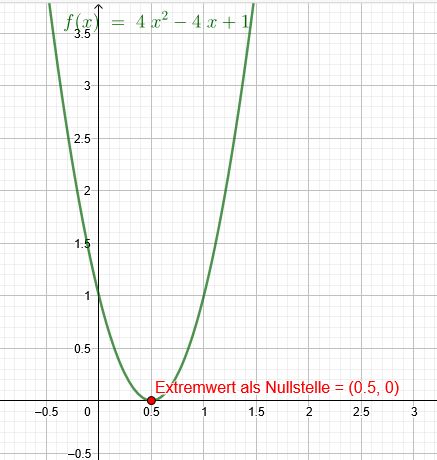
$4 x^{2}-4 x+1=0 |-1$

$4 x^{2}-4 x=-1 |:4$

$x^{2}-1* x=-\frac{1}{4}$

$( x-\frac{1}{2})^2=-\frac{1}{4}+\frac{1}{4}=0 |\sqrt{~~}$

1.) $x-\frac{1}{2}=0 |$

 $x_1=\frac{1}{2}$

2.) $x-\frac{1}{2}=-0$  Ich führe den Minuswert auf, weil es auch z.B. $\sqrt{9}$ heißen könnte.

 $x_2=\frac{1}{2}$

Das Ergebnis ist somit eine doppelte Nullstelle, die auf einen Extremwert hinweist.

Comments

Als Ergänzung:

Binomische Formeln können hilfreich sein.

4x²-4x+1 =(2x-1)²=0 → x=½

Answer 2

z.B.:

$8 x-4=-3 x+4 |+3x$  

$11 x-4=4 |+4$

$11 x=8 |:11$

$x= \frac{8}{11}$

oder auch

$\frac{1}{7} x^{2}-6=1 |\cdot 7$

$x^{2}-42=7 |+42$

$x^{2}=49$

$x=7$  oder  $x=-7$