Aufgabe:
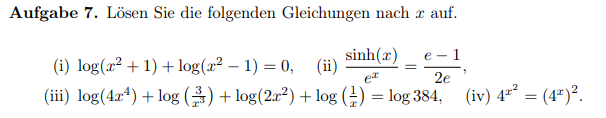
Text erkannt:
Aufgabe 7. Lösen Sie die folgenden Gleichungen nach \( x \) auf.
(i) \( \log \left(x^{2}+1\right)+\log \left(x^{2}-1\right)=0 \),
(ii) \( \frac{\sinh (x)}{e^{x}}=\frac{e-1}{2 e} \),
(iii) \( \log \left(4 x^{4}\right)+\log \left(\frac{3}{x^{3}}\right)+\log \left(2 x^{2}\right)+\log \left(\frac{1}{x}\right)^{e}=\log 384 \),
(iv) \( 4^{x^{2}}=\left(4^{x}\right)^{2} \)
Problem/Ansatz:
Die i) habe ich gelöst, indem ich durch exp geteilt habe.
Nun bin ich bei der ii) und weiß nicht weiter. Ich vermute mal ich muss durch log teilen, aber so richtig klappt das nicht.
Die iii) und iv) würde ich glaube ich wieder selbst hinbekommen.