Diese Antwort ist speziell für @Moliets und der Versuch, ihm zu zeigen wie ein analytischer Beweis aussehen würde ohne weitere Annahmen über Winkel oder Verwendung von konkreten Geraden in Geogebra.
Wir wollen das Ergebnis analytisch berechnen, ohne einen rechten Winkel bei S und T anzunehmen.
Schritt 1: Wir wählen o.B.d.A ein geeignetes Koordinatensystem:
• Wir legen den Schnittpunkt T der Schenkel in den Ursprung (0, 0).
• Der erste Schenkel (mit den Punkten T, R, Q) sei die x-Achse.
• Der zweite Schenkel (mit den Punkten T, S, P) habe die Steigung m, erfüllt also die Geradengleichung y=mx
Die Länge der roten Strecke TR ist gesucht.
(Die Skizze ist nicht maßstabsgerecht)
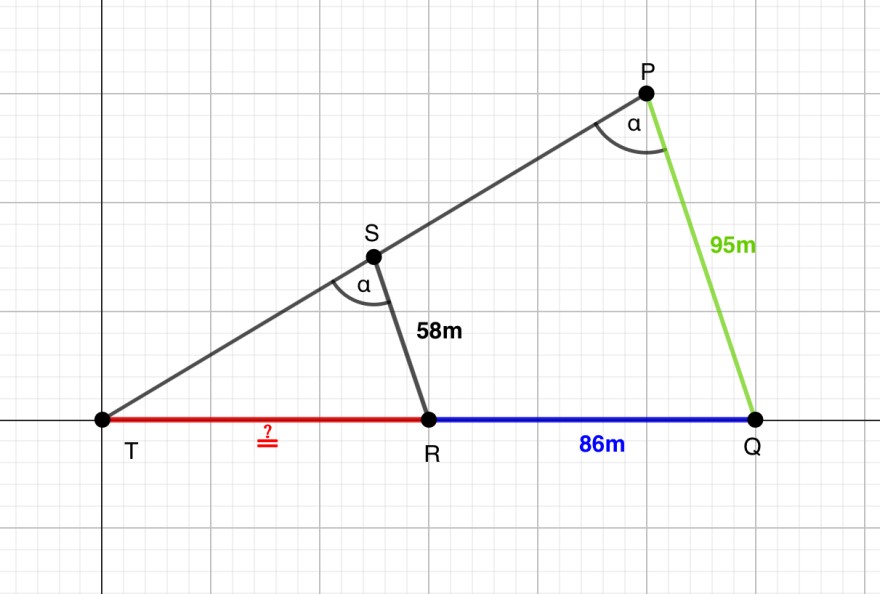
Schritt 2: Lage der Punkte
• R und Q liegen auf der x-Achse:
• R = (r,0)
• Q = (q,0)
• S und P liegen auf der Geraden durch T (also den Ursprung) mit der Form y = mx:
• S = (s,ms)
• P = (p,mp)
Schritt 3: die Strecken RS und QP sind parallel
Da RS und QP parallel sind, müssen ihre Richtungsvektoren proportional sein:
In Koordinaten:
(s-r, ms-0) = k(p-q,mp-0)
Daraus folgt:
1. s-r= k(p-q)
2. ms = kmp und daraus folgt: s = kp sowie r = kq
Schritt 4: Längen der Strecken
Die Längen RS = 58 m und QP = 95 m ergeben:
\( \sqrt{(s-r)^{2}+(ms)^{2}} \) = 58 und
\( \sqrt{(p-q)^{2}+(mp)^{2}} \) = 95
Mit s = kp und r = kq (aus Schritt 3) folgt:
58 = \( \sqrt{(k(p-q))^{2}+(kmp)^{2}} \) = \( k\sqrt{((p-q))^{2}+(mp)^{2}} \) = k*95
Somit ist der Proportionalitätsfaktor: k = \( \frac{58}{95} \)
Schritt 5:
Der Abstand QR beträgt 86 m.
Da Q = (q,0) und R = (r, 0) auf der x-Achse liegen:
lq-rl = 86
Mit r = kq (aus Schritt 3) ergibt sich:
lq - kq|= lq(1-k)|= 86
Einsetzen von k = \( \frac{58}{95} \) liefert:
q(1- \( \frac{58}{95} \)) = q\( \frac{37}{95} \) = 86 und damit q = \( \frac{86*95}{37} \)
Letzter Schritt:
Da R = (r,0) = (kq,0) (Schritt 3) folgt:
lRTl = lrl = \( \frac{58}{95} \)q = \( \frac{58}{95} \) * \( \frac{86*95}{37} \) = \( \frac{58*86}{37} \) ≈ 134,81m
Möglicherweise ist die Anwendung des Strahlensatzes einen Tick einfacher…