Trapez und Halbkreis

Question

Aufgabe:

Wie groß ist der Flächeninhalt der bananengelben Fläche, die den Halbkreis in C berührt, wenn das Verhältnis der Flächeninhalte von dunkelgrüner zu hellgrüner Fläche 3 beträgt?

(Autor: Noel Artiles-Leon, 2025)

Problem/Ansatz:

Flächeninhalt = 31,1044947... und der exakte Wert wird eine Fleißaufgabe sein. Ich habe die Aufgabe zur Unterhaltung der geneigten Mitleserschaft eingestellt.

Comments

Ja, der Wert stimmt.

A = 64·(√(a·(8 - a)) - 2)/√(a·(8 - a))

wobei hier a die x-Koordinate an der die Tangente an dem Halbkreis anliegt.

a hat also einen Wert von ca. 4.927

a habe ich so auf die schnelle allerdings auch nur numerisch bestimmt.

Schade, dass du keinen Link zum Autor und seiner Arbeit gesetzt hast.

---

Auch mein Freund Wolfram möchte das nicht exakt lösen.

---

Mehr als was in der Aufgabe steht, habe ich vom Autor nicht. Seine Abbildung habe ich neu gezeichnet.

Er vetritt die Ansicht, die exakte Lösung sei

\( \displaystyle A= \frac{1}{5}\pi \sqrt{776\pi - 186e +1123\;\ln(2) -260} \)

Das bezweifle ich.

Der Flächeninhalt nimmt, wenig erstaunlich, ab mit steigendem Verhältnis der Flächeninhalte der grünen Flächen, beginnend mit 32 bei horizontaler Tangente (Verhältnis = 1):

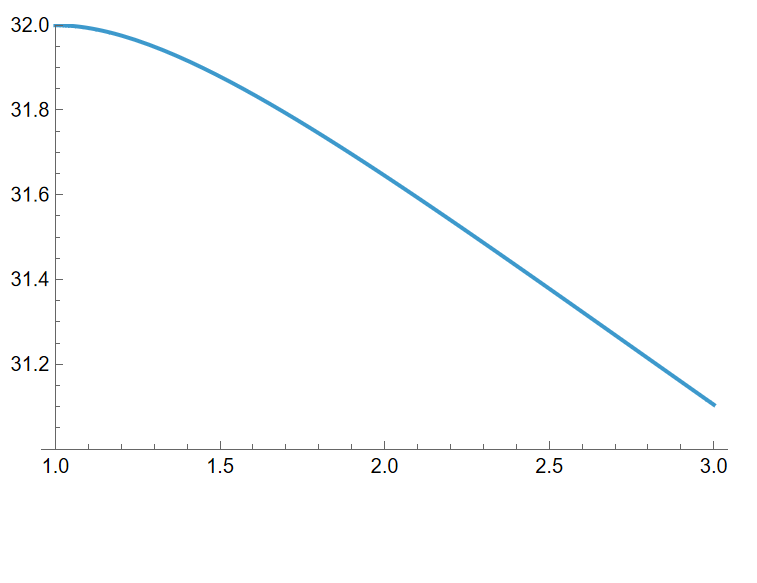
Unterhalb eines Flächeninhaltes von 24 wird das Trapez zum Dreieck.

---

Er vetritt die Ansicht, die exakte Lösung sei
\( \displaystyle A= \frac{1}{5}\pi \sqrt{776\pi - 186e +1123\ln(2) -260} \)

mein erster Gedanke dazu: wie kann das sein?

mein zweiter Gedanke: Ist das vielleicht eine Fake-Lösung? So weit ich das beurteilen kann, ist die Lösung bis auf 10 Stellen hinter dem Komma korrekt. Andererseits kann man mit einem Term der Art$$\frac{\pi}{k_0}\sqrt{k_1\pi + k_2e + k_3\ln(2) + k_4}$$mit der Wahl der 'richtigen' Koeffizienten \(k_i\) ziemlich viele Zahlen 'treffen'. Auch dann wenn man die Bedingungen \(-1000 \le k_i \le 2000 \) sowie \(k_i \in \mathbb{Z}\) vorsieht.

@döschwo : Zu welchem Datum wurde diese Lösung veröffentlich? War das vielleicht der 1.April? Ist dieser Herr Artiles-Leon vielleicht Nummeriker?

Also wenn das kein Fake ist, wäre ich brennend an der Herleitung dieses Ergebnisses interessiert. Da muss eine Art Mathematik drin stecken, von der ich bisher nichts weiß.

---

Die Aufgabe ist aus der facebook-Gruppe "Mathematics For Everyone" vom 17.7.2025

---

Ich sag nur: Cleo 2.0

---

Hallo Werner, ich dachte bei der angegebenen exakten Lösung auch an Humor. Sie wurde am 28.7.2925 vom Autor der Aufgabe ohne Herleitung veröffentlicht in der von Nudger genannten Facebook-Gruppe. Der Mann ist Ingenieur und seit 1997 Professor am Industrial Engineering Department, University of Puerto Rico.

Ich komme auf 13 übereinstimmende Nachkommastellen. Also wird die exakte Lösung falsch sein.

---

Der Mann ist Ingenieur und seit 1997 Professor am Industrial Engineering Department, University of Puerto Rico.

Das findet man zwar im Internet, das mit dem Prof hält aber keiner Überprüfung stand.

---

Bei seiner angegebenen Uni habe ich seinen Namen hier gefunden.

Wenn er 1989 promoviert wurde, dann dürfte er etwa im Pensionsalter stehen, und vielleicht noch in einzelne Lehrveranstaltungen eingebunden sein.

---

Vorgestern hab ich ihn auf den Uni-Seiten nicht gefunden. Der angegebene Link funktioniert bei mir nicht (keine Verbindung). Irgendwo fand ich "Bachelor 1979", ja, Pensionsalter. Was das an einer Uni in Puerto Rico bedeutet, weiß ich nicht.