das hier ist nur eine Ergänzung und wurde ähnlich auch so schon beschrieben.
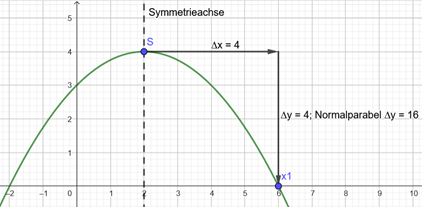
Über die Symmetrieachse wird der zweite Nullpunkt klar, das Verhältnis von Δx zu Δy zeigt, dass die Parabel um den Faktor 4 gestaucht und natürlich nach unten geöffnet ist, also:
\(f(x)=-\frac{1}{4}(x+2)(x-6)\) umgestellt \(f(x)=-\frac{1}{4}x^2+x+3\)
mir ist die faktorisierte Form ins Auge gesprungen; vielleicht ist die ja noch bei solchen Aufgeaben präsent. Solche Aufgaben werden schon gestellt, bevor Extrempunkte mit \(f'(x)=0\) bestimmt werden.