Ich habe in meinem Buch (Vorkurs der Ingenieurmathematik) unter Trigonometrie über viele Seiten etliche Erläuterungen, Beziehungen, Herleitungen, Eigenschaften, Gleichungen, Funktionswerte, Funktionen, Formeln, Tabellen, Graphen etc., stehen.
Doch da sind viel zu wenig Beispiel-Aufgaben mit Lösungsweg und ich habe kaum Erfahrung, um die nachträglichen Aufgaben allein mit den Darstellungen lösen zu können. Dazu würde es mehr als nur logische Verknüpfungen und ständiges hin und her Blättern benötigen. (Einige konnte ich so lösen)
Ich brauch ein grundlegendes Verständnis und eine gute Übersicht. Das habe ich bisher allein mit dem Buch meist gut geschafft, und alle Aufgaben lösen können, nur bei der Trigonometrie habe ich kaum noch Durchblick.
Gibt es eine Seite zur Hilfe? Habt Ihr wertvolle Tipps?
Ich würde gerne über eure Herangehensweise in der Vergangenheit erfahren.
Hier sind die Aufgaben, damit ihr ein Bild vom Niveau habt:
10.3 Man beweise die Beziehung \( \frac{1}{\cos ^{2} \alpha}=1+\tan ^{2} \alpha \)
10.4 Gegeben ist \( \sin \alpha=\frac{1}{k} . \) Man berechne \( \cos \alpha, \tan \alpha, \cot \alpha \).
10.5 Man vereinfache
a) \( y=\sin \left(x+\frac{\pi}{2}\right) \)
b) \( \quad y=\cos \left(x-\frac{\pi}{2}\right) \)
c) \( y=\tan \left(x+540^{\circ}\right) \)
d) \( \frac{\cos \left(90^{\circ}+\lambda\right)}{\cos \left(180^{\circ}+\lambda\right)} \)
10.6 Die folgenden Terme sind zu vereinfachen
a) \( \cos \left(45^{\circ}+\beta\right)-\cos \left(45^{\circ}-\beta\right) \)
b) \( \sin \left(120^{\circ}+\alpha\right)+\cos \left(210^{\circ}-\alpha\right) \)
c) \( \frac{\sin \alpha}{1-\cos \alpha} \)
d) \( \frac{(1-\cos \alpha) \cos \alpha}{\sin 2 \alpha} \)
e) \( \frac{\sin \alpha+\sin \beta}{\cos \alpha+\cos \beta} \)
10.7 Man beweise die folgenden Gleichungen
a) \( \sin \alpha+\sin \left(\alpha+120^{\circ}\right)+\sin \left(\alpha+240^{\circ}\right)=0 \)
b) \( \tan \alpha+\cot \alpha=\frac{2}{\sin 2 \alpha} \)
c) \( \sqrt{\frac{1-\cos \beta}{1+\cos \beta}}=\tan \frac{\beta}{2} \)
d) \( \frac{1+\tan \alpha}{1-\tan \alpha}=\tan \left(45^{\circ}+\alpha\right) \)
e) \( \sin 3 x=3 \sin x-4 \sin ^{3} x \)
10.8 Man bestimme \( \alpha \) in den ersten vier Quadranten
a) \( \sin \alpha=0,5314 \)
b) \( \cos \alpha=-\frac{1}{2} \sqrt{3} \)
c) \( \tan \alpha=0,7500 \)
d) \( \cot \alpha=-1 \)
e) \( \sin \alpha=-0,3736 \)
f) \( \cos \alpha=0,9510 \)
10.9 Man vereinfache
a) \( \arctan \sqrt{\frac{1-\cos 2 x}{1+\cos 2 x}} \)
b) \( \arccos (\sin x) \)
10.10 Man löse die folgenden goniometrischen Gleichungen (Es sind nur die Hauptwerte anzugeben)
a) \( 4 \sin x+3=0 \)
b) \( 2 \sin 2 x-\sqrt{3}=0 \)
c) \( \sin x-\cos x=1 \)
d) \( \sqrt{3} \cos x+\sin x-1=0 \)
e) \( 4 \sin x=6 \cot x \)
f) \( 3 \cos ^{2} x+\sin x \cos x+2 \sin ^{2} x=3 \)
g) \( \cos 2 x+\cos x=0 \)
h) \( \sin 2 x-\cos x=0 \)
i) \( 1-\cos x=\frac{1}{3} \tan \frac{x}{2} \)
k) \( \sqrt{3} \cos 2 x=\sin x-\sqrt{3} \)
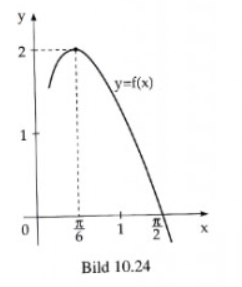
10.11 Für die in Bild \( 10.24 \) gezeigte Funktion gelten die Beziehungen:
\( f(x)=a \sin (\omega x+\varphi)=a \cos (\omega x+\psi) \)
\( =b_{1} \sin \omega x+b_{2} \cos \omega x \).
Man berechne \( a, \omega, \varphi, \psi, b_{1} \) und \( b_{2} \).
Gegeben sind die drei Ströme
\( i_{1}=25 \mathrm{~A} \sin \omega t, i_{2}=10 \mathrm{~A} \sin \left(\omega t+\frac{\pi}{2}\right), i_{3}=15 \mathrm{~A} \sin (\omega t+\pi) \)
Man berechne den resultierenden Strom \( \vec{i}=i_{1}+i_{2}+i_{3}=\hat{i} \mathrm{~A} \sin (\omega t+\varphi) \)