Ich rechne einfach das Teilstück des Umfangs aus:
Hier ein Bild als Übersicht:
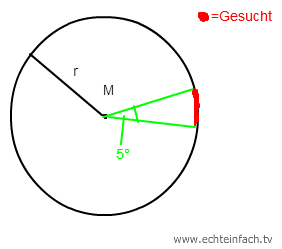
Zuerst muss man den gesamten Umfang ausrechnen:
U = 2rπ = 2*π*6378 = 40074.15589km
Dies entspricht ja 360°, wir brauchen aber nur 5°. Alos nehmen wir den Umfang mit 5/360 mal:
U*5/360 = 556.5854985km
und dies ist schon die Lösung!
Ich hoffe, ich konnte helfen und du verstehst es jetzt!
Simon