Eine 4x4 Matrix ist diagonalisierbar, wenn sie 4 linear unabhängige Eigenvektoren besitzt.
Also müssen wir Eigenwerte und Eigenvektoren der Matrix bestimmen:
Für die Ermittlung der Eigenwerte müssen die Nullstellen des charakteristischen Polynoms bestimmt werden.
$$ O = \operatorname { det } \left( \begin{array} { c c c c } { 1 - \lambda } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 1 - \lambda } & { 0 } & { 0 } \\ { - 1 } & { 1 } & { 1 - \lambda k } \\ { 0 } & { 0 } & { 1 } & { - \lambda } \end{array} \right) \\ = ( 1 - \lambda ) \cdot \operatorname { det } \left( \begin{array} { c c c } { - 1 - \lambda } & { 0 } & { 0 } \\ { 1 } & { 1 - \lambda } & { k } \\ { 0 } & { 1 } & { - \lambda } \end{array} \right) \\ = ( 1 - \lambda ) \cdot ( - 1 - \lambda ) \cdot \operatorname { det } \left( \begin{array} { c } { 1 - \lambda } & { k } \\ { 1 } & { - \lambda } \end{array} \right) \\ = ( 1 - \lambda ) ( - 1 - \lambda ) \left( \lambda ^ { 2 } - \lambda - k \right) $$
Die Nullstellen kann man nun direkt ablesen:
λ1 = 1
λ2 = -1
λ3 = 1/2 + √(1/4+k)
λ4 = 1/2 - √(1/4+k)
Da zu jedem unterschiedlichen Eigenwert mindestens ein Eigenvektor existiert, ist die Matrix auf jeden Fall diagonalisierbar, wenn alle vier Lösungen unterschiedlich sind.
Zusammenfallen können aber nur λ1 und λ3 oder λ2 und λ4 oder λ3 und λ4.
Wenn λ1 und λ3 zusammenfallen gilt:
1 = 1/2 + √(1/4+k)
1/2 = √(1/4+k)
1/4 = 1/4 + k
k = 0
Untersuchen wir also den Fall k = 0:
Dann gilt:
λ1 = 1
λ2 = -1
λ3 = 1
λ4 = 0
Zu λ2 und λ4 existieren zwingend Eigenvektoren, also ist zu prüfen, wie viele Eigenvektoren zu λ=1 existieren.
Es muss also der Kern der Matrix A-1*E bestimmt werden. Das mache ich mit dem Gaußalgorithmus:
$$ A - E = \left( \begin{array} { c c c c } { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { - 2 } & { 0 } & { 0 } \\ { - 1 } & { 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 1 } & { - 1 } \end{array} \right) \sim \left( \begin{array} { c c c c } { 1 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { - 2 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 1 } & { - 1 } \end{array} \right) \sim \left( \begin{array} { c c c c } { 1 } & { - 1 } & { 0 } & { 0 } \\ { 0 } & { 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 1 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } \end{array} \right) \sim \left( \begin{array} { c c c } { 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 1 } & { - 1 } \\ { 0 } & { 0 } & { 0 } & { 0 } \end{array} \right) $$
Der Kern besteht nur aus den Vielfachen des Vektors (0,0,1,1) also existieren nur 3 linear unabhängig Eigenvektoren: die Matrix ist für k=0 nicht diagonalisierbar.
Ebenso verfährt man für die Fälle λ2 = λ4 ⇒ k = 2 und λ2 = λ4 ⇒ k = -1/4.
Man stellt fest, dass dann wieder nur drei Eigenvektoren existieren.
Die Matrix ist also diagonalisierbar für alle k∈ℝ\{0, 2, -1/4}
Aufgabe 9a)
Zu prüfen sind die Gruppenaxiome:
I) Assoziativität A+(B+C) = (A+B)+C
II) Existenz des neutralen Elements 0 mit A+0 = 0+A = A
III) Existenz des Inversen Elements -A mit A+(-A) = 0
IV) Kommutativität: A+B = B+A
Das beweist man alles sehr leicht mit den Regel der Matrizenaddition:
I)
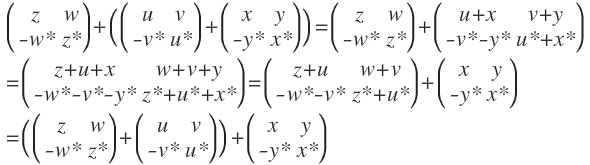
II) Das neutrale Element ist die Nullmatrix. Es ist leicht zu sehen, dass sie in H liegt und die Bedingung erfüllt.
III) Das inverse Element zu A = ((z, w),(-w*, z*)) ist
-A = ((u, v),(-v*, u*)) = ((-z, -w),(w*, -z*))
also u=-z, v = -w.
Man sieht wieder leicht, dass A+(-A) = 0 gilt.
IV) Kommutativität zeigt man genauso wie Assoziativität. Sie folgt aus den Gesetzen der Matrizenaddition und den Regeln der Addition reeller Zahlen.
b) Es sind dieselben Axiome zu prüfen, diesmal aber für die Matrizenmultiplikation (also statt + jetzt · ). Ich verkürze das mal ein bisschen.
I) Ist erfüllt, weil die Matrizenmultiplikation assoziativ ist.
II) Das neutrale Element ist die Einheitsmatrix. Sie liegt in H und erfüllt 1*A = A*1 = A für alle A aus H (wobei 1 die Einheitsmatrix ist)
III) Wegen det A = z·z* + w·w* = |z|² + |w|² > 0 ist jede Matrix in H\{0} (wobei 0 die Nullmatrix ist) invertierbar.
Das Inverse lautet
$$ A ^ { - 1 } = \frac { 1 } { | z | ^ { 2 } + | w | ^ { 2 } } \left( \begin{array} { c } { z ^ { * } - w } \\ { w ^ { * } z } \end{array} \right) $$
Sie liegt in H und durch nachrechnen zeigt man leicht, dass A-1A = 1 gilt.
IV) Um zu prüfen, ob die Gruppe abelsch ist, berechne ich den Kommutator
[A, B]- = AB - BA
Nur wenn der Kommutator für alle A und B die Nullmatrix ergibt, ist die Operation kommutativ und die Gruppe abelsch.
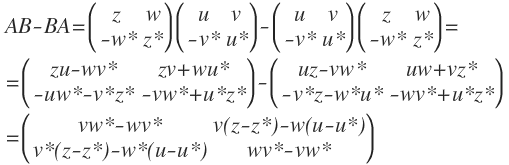
Wegen vw* - wv* = Im(vw*) erkennt man leicht, dass z.B. für v = 1, w=i diese Komponente des Kommutatotors nicht verschwindet.
Also gilt nicht für alle A und B
AB = BA
die Gruppe ist damit nicht abelsch.