Ermittle die Gleichung des Inkreises: A(1/-11) B(4/-5) C(-4/-1)

Question

Ich brauche ganz  Hilfe :( Ich hab nämlich keine Ahnung, wie ich den Inkreis eines Dreiecks berechnen soll. A(1/-11) B(4/-5) C(-4/-1) Danke fürs helfen

Comments

Den Inkreismittelpunkt kann man konstruieren, indem man die Winkelhalbierenden schneidet. Er hat von allen 3 Geraden denselben Abstand.

Hast du eventuell eine Formel, mit der du den Abstand eines Punktes von einer Geraden bestimmen kannst. 3-dim. wäre die Hessesche Normalform HNF ideal.

Wenn ja, kannst du M(mx|my) in alle HNF einsetzen. und je 2 von denen gleichsetzen.

Answer 1

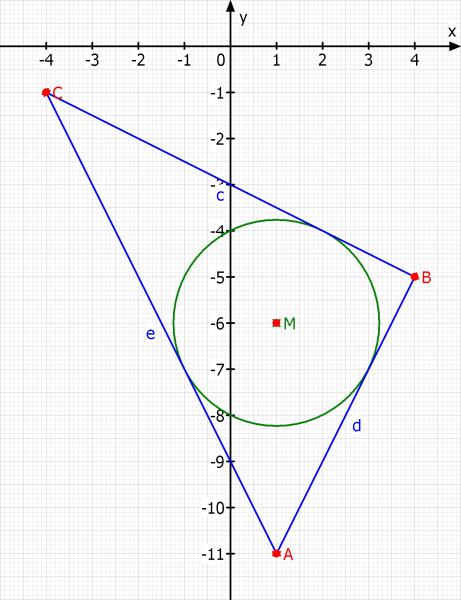
A [1,-11]
B [4, -5]
C [-4, -1]

Winkelhalbierende bei A

x = A + r * AB / |AB| + r * AC / |AC|
x = [1, -11] + r·([4, -5] - [1, -11])/ABS([4, -5] - [1, -11]) + r·([-4, -1] - [1, -11])/ABS([-4, -1] - [1, -11])
x = [1, 4·√5·r/5 - 11]

Winkelhalbierende bei B

x = B + r * BA / |BA| + r * BC / |BC|
x = [4, -5] + r·([1, -11] - [4, -5])/ABS([1, -11] - [4, -5]) + r·([-4, -1] - [4, -5])/ABS([-4, -1] - [4, -5])
x = [4 - 3·√5·r/5, - √5·r/5 - 5]

Schnittpunkt heißt die Winkelhalbierenden gleichsetzen

[1, 4·√5·r/5 - 11] = [4 - 3·√5·s/5, - √5·s/5 - 5]

Lösung des LGS ist r = 5/4·√5 ∧ s = √5

Setzte ich das nun in eine Gleichung ein habe ich den Umkreismittelpunkt

M = [1, 4·√5/5·(5/4·√5) - 11] = [1, -6]

Abstand Dieses Punktes von einer Geraden ist der Radius.

d = (AB x AM)/|AB|
d = ([4, -5] - [1, -11]) ⨯ ([1, -6] - [1, -11])/ABS([4, -5] - [1, -11])
d = √5

Damit lautet die Kreisgleichung 

(x - 1)^2 + (y + 6)^2 = 5

Hier eine Skizze:

Comments

Sehr schön.

NB. Du wolltest doch schreiben "Schnittpunkt heißt die Winkelhalbierenden gleichsetzen"

---

Ja. Hm. Was sind den Winkelsenkrechten? Keine Ahnung wie ich auf das Wort gekommen war :)

---

Man hätte den Mittelpunkt des Inkreises und den Radius auch über eine einfache Formel bekommen können. Ich habe darauf mal im Rahmen der analytischen Geometrie verzichtet.

Für Leute die aber gerne Formeln mögen verweise ich daher an dieser Stelle auf

https://de.wikipedia.org/wiki/Inkreis

Answer 2

Hi,

es gilt r=2A/u

Wir brauchen also die Längen der Seiten.

Seite AB:

(4-1)=3 und -5-(-11)=6 -> c^2=3^2+6^2=45

Seite BC:

(4-(-4))=8 und -1-(-5)=4 -> a^2=8^2+4^2=80

Seite AC:

(1-(-4))=5 und (-11-(-1))=-10 -> b^2=5^2+10^2=125

 

Nun mit der heronschen Flächenformel A errechnen:

A=√(s(s-a)(s-b)(s-c))=30

mit s=(a+b+c)/2

 

r=2A/u=2,24

 

Grüße

 

Nachtrag: Ups, ich hab die Frage falsch verstanden. Mein Weg ist zwar nicht falsch, aber unnötig aufwendig, wenn man die Kreisgleichung wünscht.

Siehe Lu und Mathecoach