Quadratische Pyramide: Seitenlänge 6 cm, Höhe 4 cm, Oberfläche?

Question

Die Grundfläche einer Pyramide ist ein Quadrat mit 6 cm Seitenlänge. Die Pyramide ist 4 cm hoch. Bestimme zuerst die Hohe der Seitendreiecke, dann die Oberfläche der Dreiecke.

Die Höhe der Seitendreiecke habe ich schon 5cm. Nur wie krieg ich die Oberfläche raus? In der Lösung steht: O=36+65+65=96

Aber die Formel ist doch O=G+M

Realschule...

Answer 1

Die Formel ist richtig.

Die Grundfläche ist das Quadrat, also

G = 6cm*6cm = 36cm²

Der Mantel besteht aus vier Dreiecken mit der Grundseite g 6cm und der Höhe h 5cm. Der Flächeninhalt eines Dreiecks lautet: (g*h)/2

M = 4*(6cm*5cm)/2 = 4*(30cm²)/2 = 60cm²

 

Für die ganze Oberfläche gilt damit:

O = G+M = 36cm²+60cm² = 96cm²

Answer 2

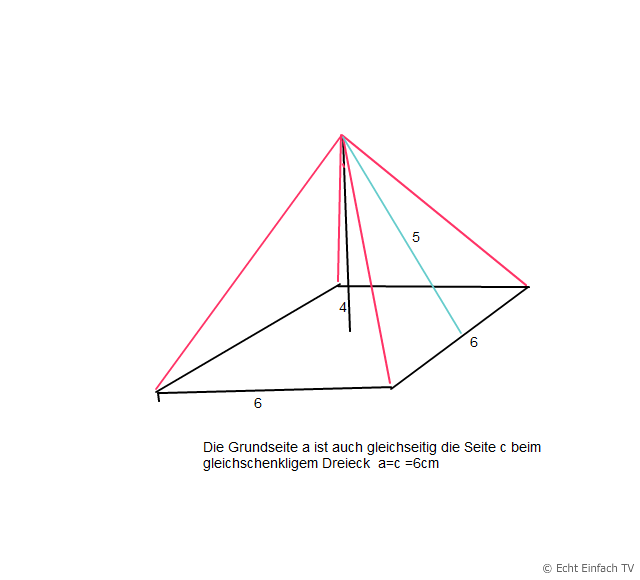
Da stimmt etwas nicht mit der Lösung , denn O =36+65+65=166, das Endergebnis mit 96 ist allerdings richtig.

Die Grundfläche der Pyramide ist ja ein Quadrart mit der Kantlänge 6 und der Mantel sind 4 gleichschenkliges Dreieck mit  mit c=6 und h_c=5 , das Ergebnis stimmt.

G=6*6=36

M=4(1/2*c*h_c)=  4*0,5*6*5=4*15=60

O=G+M=36+60=96

die Oberfläche beträgt 96cm².