Konvergenz und absolute Konvergenz: Wurzelkriterium? Summe von (-1)^n (2n tief n)

Question

Quotientenkriterium

EDIT(Lu): Überschrift und Tags dem Fragetext angepasst. 

1.

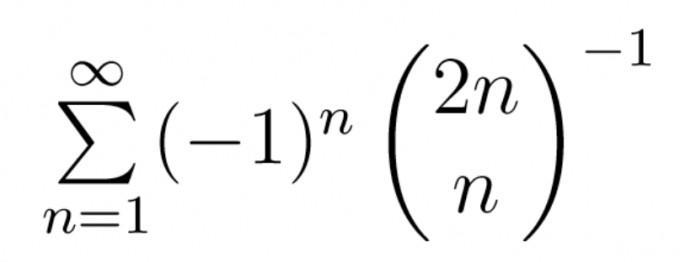
2.

 

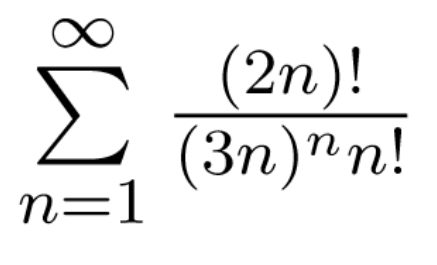
3.

 

Alle drei Reihen soll ich mit dem Wurzelkriterium auf konvergenz und absolute Konvergenz untersuchen.

die 3. Reihe soll divergieren, die 1. und 2. sollen konvergieren

Kann mir jemand weiter helfen - wie ich das machen kann. vielen dank

Comments

In der Überschrift steht Quotienten-Krit. in deiner Frage Wurzel-Krit.

---

EDIT: Habe mal die Überschrift der Frage angepasst. 

Die drei Reihen wurden ja schon öfters gefragt. Kann sein, dass man die Fragestellung (inkl. Lösung) findet, wenn man geschickt sucht. 

---

Ich finde die Reihen nicht -
hier in dem forum wurden es gefragt weißt du vielleicht noch ca wann ?

---

Nr. 1 ist eine alternierende Reihe. Die Summanden bilden eine Nullfolge.

==> Die erste Reihe konvergiert. 

---

Zur absoluten Konvergenz bei (1) zeige z.B., dass
\(\dfrac{\binom{2n}{n}}{\binom{2(n+1)}{n+1}}=\dfrac{n+1}{4n+2}\le\dfrac13\) für alle \(n\ge1\) gilt.

---

Ist es richtig, dass bei der (2) durch das Quotientenkriterium 1/2 < 1 rauskommt (und daher abs. konv., wobei das ja bereits in der Frage bestätigt wurde)

---

bei der (2) müsste mit Quotientenkriterium 4/3e < 1 rauskommen. Demnach absolut konvergent.