Kegelschnitte. Quadratische Ergänzung zur Erkennung worum es geht

Question

Ich habe hier ein Beispiel. Es ist gefragt, ob die Relation der zwei Gleichungen a und b

Hyperbeln, Ellipsen oder Parabeln entspricht.

a) 2x+x²+1-4y+y²=0

sowie

b) 4x²-8x+84+54y+9y²=0

Es sollen Parameter wie "Achsenlängen". "Scheitel", Asymptoten usw. bestimmt werden, Relationen grafisch dargestellt werden inkl. den Bildbereich B

und der Definitionsbereich D der Grafik soll abgelesen werden.

über Hilfe eurerseits würde ich mich freuen!lg!!

Answer 1

a)  Den Kreis hast du ja schon bei Mathecoach

b)

4x² - 8x + 84 + 54y + 9y² = 0   | +1 | 85 links auf quadratische Ergänzungen * Vorfaktor aufteilen

Ausklammern und quadratisch ergänzen:

4 * (x² - 2x + 1² ) + 9 * (y² + 6y + 3²) = 1           Ergibt  84 + 1 = 85

       (x-1)² / (1/4) + (y+3)² / (1/9) = 1

      (x-1)² / (1/2)² + (y+3)² / (1/3)² = 1

ist eine Ellipse  (x - x_m)² / a² + (y - y_m)² / b² = 1

mit dem Mittelpunkt (1|-3) und den Halbachsen a = 1/2  und  b = 1/3

Gruß Wolfgang 

Answer 2

2·x + x^2 + 1 - 4·y + y^2 = 0

x^2 + 2·x + 1 + y^2 - 4·y + 4 = 4

(x + 1)^2 + (y - 2)^2 = 2^2

Das ist ein Kreis. Kannst du die Lageparameter ablesen?

Comments

4·x^2 - 8·x + 84 + 54·y + 9·y^2 = 0

4·(x^2 - 2·x) + 9·(y^2 + 6·y) = -84

4·(x^2 - 2·x + 1) + 9·(y^2 + 6·y + 9) = -84 + 4 + 81

4·(x - 1)^2 + 9·(y + 3)^2 = 1

(x - 1)^2 / 0.5^2 + (y + 3)^2 / (1/3)^2 = 1

Das ist eine Ellipse. Kannst du die Lageparameter ablesen?

---

Erschreckend wie klar das jetzt ist.

Answer 3

\(f(x,y)=4·x^2 - 8·x + 84 + 54·y + 9·y^2 \)

\(f_x(x,y)=8x - 8 \)  

\(f_y(x,y)= 54 + 18y\)

Mittelpunkt der Ellipse:

\(8x - 8=0\)    →\(x=1\)

\( 54 + 18y=0\)   →\(y=-3\)

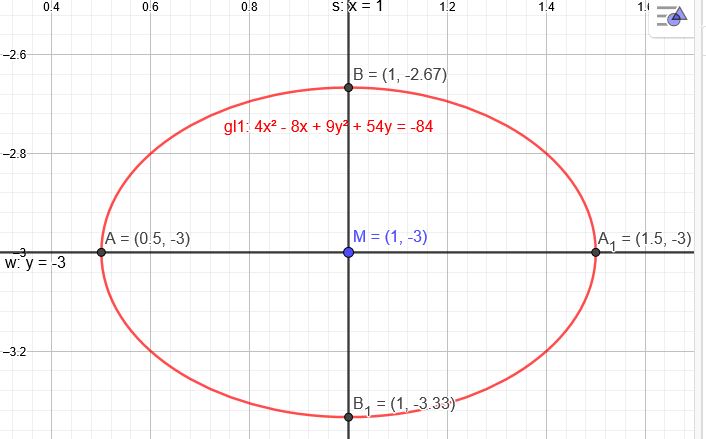
\(M(1|-3)\)

Achsenlängen:→Hauptachse:

\(4·x^2 - 8·x + 54·y + 9·y^2=-84 \)    mit   \(y=-3\) :

 \(4·x^2 - 8·x + 54·(-3) + 9·(-3)^2=-84 \) 

\(x_1=0,5 \)     \(x_2=1,5 \)      → \(2a=1\)        → \(a=0,5\) 

Nebenachse:

\(4·x^2 - 8·x + 54·y + 9·y^2=-84 \)    mit   \(x=1\) :

\(4 - 8 + 54·y + 9·y^2=-84 \)

 \(y_1=-\frac{10}{3} \)       \(y_2=-\frac{8}{3} \)    \(2b=\frac{2}{3}\)        → \(b=\frac{1}{3}\)

Comments

Für wen ist diese Antwort?

---

Für wen ist diese Antwort?

Für Leser und Leserinnen, die darauf stoßen.