Zirkuszelt mit Lichtkreis. Das Volumen von Rotationskörpern 3

Question

Stimmen meine Lösungen? Ich brauche Hilfe bei der Aufgabe.

 

 

Comments

 Ich brauche Hilfe bei a)-d). Es reicht der Ansatz und die direkte Lösung zum Vergleichen.

Analysis. Zirkuszelt entsteht durch Rotation des Flächenstücks um die y-Achse 

---

Außenwand*                                                     

---

Probe, wann lernst du, endlich mal die TeX-Vorschau

https://www.matheretter.de/rechner/latex

anstelle dieser Grafik-TeX-Hilfskrücke zu benutzen?

Answer 1

Hallo Schwesterlein, 

a) 

die Umkehrfunktion ist richtig

b)  

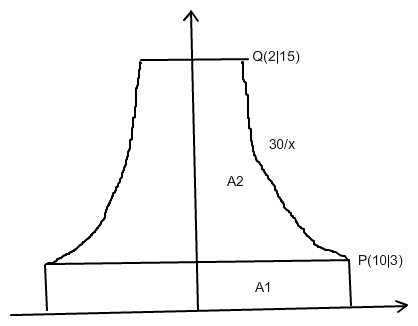
Die Punkte P(10|3) und Q(2|15) hast du offensichtlich richtig erkannt.

Das Zeitvolumen ergibt sich aber aus dem  Rotationsvolumen der Fläche A2 um die y-Achse und dem Rotationszylinder des Rechtecks A1:

V = π · ₃∫¹⁵ (30/x)² dx  + π · 10² · 3

c)

V_oben = π · ₁₀∫¹⁵ (30/x)² dx 

Prozentsatz  =  V_oben /  V  · 100%

d)

Wenn das Zeltvolumen wegen der Heizenergie möglichst klein werden soll, sollte der Punkt P möglichst niedrig liegen → P ' (10|2)

Für die neue Funktion f gilt dann  f(10) = k/10 = 2  → k = 20   →  f(x) = 20/x

Wegen f(2) = 20/2 = 10  ergibt sich dann für Q  der tiefere Punkt Q '(2/10)

V_neu =  ₂∫¹⁰  (20/x)² dx  + π · 10² · 2

Gesuchter Prozentsatz =  ( V - V_neu ) / V  · 100%

Gruß Wolfgang

Comments

Wie kommst du hier auf die untere Grenze 10?

c)

V_oben = π · ₁₀∫¹⁵ (30/x)² dx

---

Mir ist das jetzt klar.                      

---

Freut mich.  (Kommt Zeit, kommt Rat :-))

---

Wolfgang?                  

Answer 2

b)

Ich denke das Volumen ist bereits verkehrt und dabei ist das Integral richtig.

Überlege dir was dir zum Volumen noch fehlt und wie du es berechnest. Schlage dabei die Formeln zum berechnen von Körpern aus der Mittelstufe nach.

c)

Kannst du im Bild überlegen welche Luftmolekühle sich innerhalb des Zeltes in einer Höhe von mind. 10 m befinden ? Skizziere den Körper ein und überlege dir dann, wie du das Volumen berechnen kannst.

d)

Wobei hast du hier Schwierigkeiten? Gehe davon aus das das k so zu wählen ist, dass die Seitenwand genau 2 m hoch ist.

Skizziere dir das dabei entstehende Zelt auch auf.

Comments

           

Answer 3

Mit der Zeltfunktion komme ich nicht klar

Unten fängt das Zelt bei ( 10 | 3 ) an.
Oben wäre es ( 3 | 10 )

Der Lichtkreis oben müße d = 6 m betragen.
Die untere Höhe ( Zylinder ) ebenfalls 3 m.

b. Funktion = Umkehrfunktion.

Comments

> Oben wäre es ( 3 | 10 ) 

Warum nicht (2|15)  und die Zirkuswelt ist in Ordnung :-)