Question

Klausuraufgabe ( Sattelpunkt bestimmen ) mit Parameter: f_(a)(x) = (x^2 + 1/2) e^{ax}

 Ich hab schon alles probiert, komme jedoch immer auf f"a(x) = x^2 + 4x/a + 2,5 = 0

Comments

Die Ableitungen habe ich schon berechnet. Die Nullstellen von der zweiten Ableitung jedoch kann ich nicht berechnen. Wäre nett, wenn jemand sich die Mühe machen würde.

---

Du hast bestimmt gemeint "Du hast sie dir berechnen lassen"?

Wenn was unklar ist stelle keine neue Frage mit Behauptungen, sondern frage dort nach.

---

Du hast bestimmt gemeint "Du hast sie dir berechnen lassen"?

Er hat sie durchaus selbst berechnet, allerdings dann 2 nicht durch a^2 dividiert.

---

Nein das habe ich absolut nicht gemeint. Ich weiß auch nicht warum "Ronald" sich die Mühe gemacht hat, und sie nochmal abgeleitet hat, denn wie man in meiner Frage ablesen konnte, stand da schon die zweite Ableitung. Zu deinem zweiten Punkt muss ich hinzufügen, dass ich nach den Nullstellen gefragt habe, um später den Sattelpunkt identifizieren zu können.

---

EDIT: @Philippe: Gehört das hier https://www.mathelounge.de/433953/nullstellen-und-sattelpunkt-bestimmen-fa-4ax-2-fa-x-x-2-4x-2-2-a auch noch irgendwie hier dazu oder ist das eine eigene Aufgabe? Dort fehlt f.

---

Das habe ich nicht geschrieben. Womöglich ein Kommilitone.

---

@Phillipe: Tut mir leid so harsch gewesen zu sein.  Manchmal nervt mich das Lösungen-Abgehole und dann weitere Posts zu machen um fremde Arbeit als eigene auszugeben. Sry :)

---

Ich erkenne keinen Sattelpunkt.

---

Ich sehe keine Sattelpunkte oder Extrempunkte

alpha = -2, -1, 1 , 2

---

Du darfst natürlich nicht irgendein beliebiges α nehmen. Die Aufgabe besteht darin, die richtigen zu finden. x_s = +/- √2/2 .

---

Ich denke  x_S = ± √2

vgl. meine Antwort

---

Ich denke  x_S = ± √2   vgl. meine Antwort

Wenn du mal richtig hingucken würdest, könntest du sehen, dass meine Angabe richtig ist.

---

In deiner Skizze liegt x_s bei -√2 / 2 =−1/√2

---

@hj2166

Du hast - wie so oft - natürlich recht.

Sattelpunkt für a = ± √2  mit  x_S = -+ √2/2

Ich hatte im Kommentar x_S und a verwechselt, weil du "die richtigen a  finden" wolltest  :-)

Dein x_S = ± √2/2 ist deshalb aber nur bedingt richtig, weil das eben nur für  a = ± √2  gilt.

@Phillipe:

Vergleiche trotzdem meine richtige Antwort!

(Falls du das alles nach der wenig hilfreichen 1. Antwort und dem folgenden Kommentar-Hickhack überhaupt noch liest)

---

Dein x_S = ± √2/2 ist deshalb aber nur bedingt richtig, weil das eben nur für  a = ± √2  gilt.

Eben genau deshalb ist es ganz unbedingt richtig.

Answer 1

Hallo Phllipe,

die 2. Ableitung wird im Folgenden nicht benötigt.

f(x) = (x² + 1/2)·e^ax

Für  a = 0  ergibt sich

 f(x) = x² + 1/2   →  f '(x) = 2x  = 0  ⇔  x = 0   mit VZW von - → +     →   Tiefpunkt T(0|1/2)

Für a ≠ 0 ergibt sich 

f '(x) = 1/2 ·  e^ax · (2a·x²+ 4·x + a) = 0 

2a·x²+ 4·x + a = 0   ⇔    x² + 2/a ·x + 1/2 = 0  

pq-Formel →

x_1,2 = -1/a ± √(1/a² - 1/2)  für |a| ≤ √2  

Das ist ein Funktionsterm einer nach oben geöffneten Parabel.

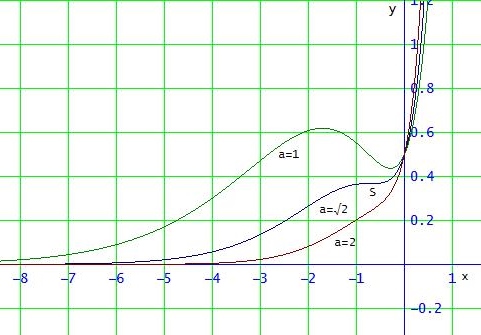
f '  hat also   keine Nullstelle für |a| > √2  →  weder Extrem- noch Sattelpunkt  

                      genau eine NS ohne Vorzeichenwechsel   für |a| = √2  →   Sattelpunkt 

                      zwei Nullstellen mit VZW  für  |a| < √2   →  2 Extrempunkte  

Gruß Wolfgang

Comments

Hallo Wolfgang,

irgendwie hat mein Matheprogramm mich genarrt.
Handschriftlich kommen bei mir auch entsprechende
Ergebnisse heraus.
Mein Matheprogramm meint(e) etwas anderes.
Irgendwo muß noch dort noch ein  Fehler sein.
Ich kann den Fehler bisher noch nicht lokalisieren.

---

Hallo Georg,

"Ein Bild sagt mehr als 1000 Worte" ist halt nicht immer richtig :-)

Matheprogramme geben bei Rechnungen  mit Parametern oft - ohne Rücksicht auf Fallunterscheidungen - einfach Terme an.

Gruß Wolfgang

---

Hallo Wolfgang,

zuerst habe ich mich rechnerisch der Aufgabe
zugewandt. Den Fehler mit dem Matheprogramm
habe ich noch immer nicht gefunden.

Die Grafiken waren nichts. Bei der gewählten
Skalierung konnte man auch nichts sehen.

Answer 2

Die erste Ableitung lautet e^αx(ax²+2x+a/2)

Die zweite Ableitung lautet e^αx(a²x²+4ax+a²/2+2).

Comments

Die zweite Ableitung lautet ...

Die wird allerdings überhaupt nicht gebraucht.

---

Das kann natürlich sein. Aber der Fragesteller hatte eine zweite Ableitung angegeben und in der Überschrift von "Sattelpunkt" gesprochen.