Bei dieser Aufgabe ist mir die Fragestellung schon ein Problem.
In einer Fabrikhalle soll ein in zwei Kammern unterteilter Lüftungskanal eingebaut werden. Der
Gesamtquerschnitt soll 3m² betragen.
Wie müssen die Maße x und y gewählt werden, wenn der
Blechverbrauch minimal werden soll?
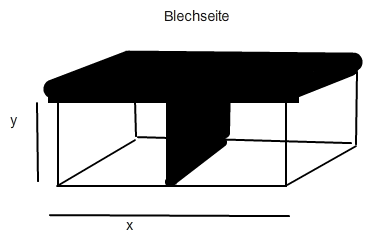
Was stellt der Gesamtquerschnitt dar? Wozu dient das Blech?
Der Rechenweg ist mir klar:
Größe die max./min. werden soll, suche -->Funktion aufstellen zwischen der Größe mit allen Angaben= Hauptbedingung
Sonstige Informationen ergeben die Nebenbedingung.
Zusammenfügen von NB in HB
Erste Ableitung bilden und gleich Null setzten --> x --> andere Variablen per Einsetzen.
Mein Problem ist das Erstellen der NB und HB, der Rest ist ja wohl nicht so schwer.
Hoffe ihr könnt mir beim Aufstellen helfen
Vielen Dank
luis