also die x_i = i entsprechen den Noten: x_1 = 1, x_2 = 2, ..., x_5 = 5.
Die h_i bezeichnen die absoluten Häufigkeiten dieser Noten, diese sind ja bereits gegeben:
h_1 = 3, h_2 = 23, ..., h_5 = 11.
Der Median ist nun die "Mitte" der Folge x_1, x_2, ..., x_5, mit anderen Worten m = x_3 (= 3).
Die mittlere absolute Abweichung ist der Durchschnitt der absoluten Abweichungen. Für das Ereignis x_1 = 1 beträgt diese zum Beispiel d_1 = |x_3 - x_1| = 2. Für x_2 ist sie d_2 = |x_3 - x_2| = 1, ..., d_5 = |x_3 - x_5| = |-2| = 2. Die mittlere absolute Abweichung d_1 ist in unserer Stichprobe h_1 = 3 Mal realisiert, für d_2 entsprechend h_2 = 23 Mal, ... und für d_5 ist sie h_5 = 11 Mal realisiert. Das heißt, um die gesamte mittlere absolute Abweichung auszurechnen, müssen wir die d_i entsprechen oft addieren, bzw. mit ihren absoluten Häufigkeiten gewichten und schließlich durch die Größe der Stichprobe n dividieren:
d = ± 1/n (h_1 * d_1 + h_2 * d_2 + ... + h_5 * d_5.)
Nach Adam Riese macht das
d = ± 79 / 100 = ± 0,79.
Die Standardabweichung ergibt sich als Wurzel der Varianz. Die Varianz ergibt sich ähnlich der mittleren absoluten Abweichung aus der Formel:
V = s^2 = Summe ( h_i * (x_i - m)^2 ). (selber ausrechnen)
Die Standardabweichung s ist dann s = wurzel(V).
Den Begriff Schiefe habe ich zwar noch nie gehört. Sie lässt sich allerdings ebenso aus einer Formel berechnen (Quelle: wikipedia.org):
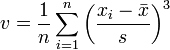
Das große Sigma ist übrigens das Summensymbol und bedeutet "Summiere über i von 1 bis n".
MfG
Mister