Hi, ich würde das schrittweise angehen...
Also zuerst einmal (x-1)2 ableiten... das wäre 2x - 2 und dann (x+1)2 ableiten: 2x + 2 und jetzt multiplizieren...
f' = (2x - 2) * (2x + 2) = 4x3 + 4x
EDIT: Kopie aus Kommentar:
Hi, ich weiß nicht weshalb meine aktualisierte Antwort nicht angezeigt wird.. aber ja, ich würde gerne den korrekten Rechengang noch einmal angeben: Also die Produktregel lautet:
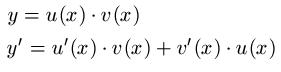
u(x) = (x-1)2
u'(x) = 2x - 2
v(x) = (x+1)2
v'(x) = 2x + 2
y' = (2x - 2) * (x+1)2 + (2x + 2) * (x-1)2 = 2x3 + 2x2 - 2x - 2 + 2x3 - 2x2 - 2x + 2
y' = 4x3 + 4x