Umformung von Termen

Question

7ab-3ac+5ac-5ab

ist dieser Term so richtig umgeformt?

20a*2b*2c ?

bitte den gesamtem Lösungsweg darstellen und erklären

Danke (-:

Answer 1

7ab-3ac+5ac-5ab

=7ab-5ab -3ac+5ac

=2ab -3ac+5ac

=2ab +2ac

=2a(b+c) 

Answer 2

Hallo Chillaxo,

"7ab-3ac+5ac-5ab ist dieser Term so richtig umgeformt? 20a*2b*2c ?" Nein!

$$\begin{aligned} & 7ab-3ac+5ac-5ab \\& = 7ab-5ab \space -3ac+5ac \\& = (7-5)ab \space +(-3+5)ac \\&= 2ab + 2ac \\&= 2a(b+c) \end{aligned}$$ Gruß Werner

Comments

danke

wie erklärt sich der schritt:

=2ab+2ac

=2a(b+c)

also mein Gehirn sagt mir dass 2*a+ 2*a 4 a ergibt und dann bleibt (b+c)

also meine falsche lösung ist:

=4a(b+c)

meine frage:

wie kommt es dazu, dass es eben nicht so ist, sondern dass es 2*a+ 2*a = 2a ergibt?

---

"wie erklärt sich der Schritt: ... also mein Gehirn sagt mir dass 2*a+ 2*a 4 a ergibt und dann bleibt (b+c)" Eine gute Frage! Und die Antwort ist:

dort steht nicht $2\cdot a + 2\cdot a$ sondern $$2a \cdot b + 2a \cdot c$$ und das ist etwas anderes! Und da ein Bild mehr sagt als tausend Worte ...

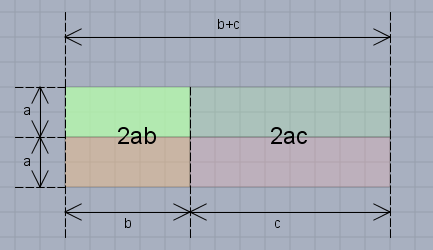
oben siehst Du vier Rechtecke. Es geht darum, die Summe aller Flächen der Rechtecke zu berechnen. Du weißt sicher schon, dass die Fläche eines Rechtecks gleich Länge mal Höhe ist. Das grüne links oben ist $b$ lang und $a$ hoch. Also ist seine Fläche $a\cdot b$. Da die beiden linken gleich groß sind, ist ihre Gesamtfläche $2\cdot a \cdot b$. Und die beiden rechts daneben haben die Fläche von $2 \cdot a \cdot c$.

Und wie groß ist nun die Fläche aller vier Rechtecke zusammen? Du kannst auch mal die Buchstaben durch Zahlen ersetzen: $a=2$, $b=5$ und $c=8$ und dann einfach mal die Kästchen zählen.