Die Winkel \(\alpha\) und \(\beta\) sind doch gegeben! Das reicht, um die Fläche des Vierecks zu berechnen.
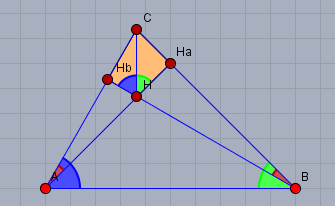
In obiger Skizze sind alle blauen Winkel \(=60°\), die grünen \(=45°\) und die roten \(=15°\). Das Dreieck \(\triangle ABH_a\) ist ein gleichschenkliges und rechtwinkliges. Also ist die Strecke
$$|H_aB| = \frac12 \sqrt{2} \cdot c$$ Demnach ist die Strecke \(|HH_a|\)
$$|HH_a| = |H_aB| \cdot \tan 15° = \frac12 \sqrt{2} \cdot c \cdot (2-\sqrt{3})$$ Damit haben wir schon mal die Fläche des Dreiecks \(\triangle HH_aC\), was ja ein 'halbes Quadrat' ist.
$$F(\triangle HH_aC) = \frac{1}{2}\left(\frac12 \sqrt{2} \cdot c \cdot (2-\sqrt{3})\right)^2 = \frac{c^2}{4}\left( 2-\sqrt{3}\right)^2 $$
Nun das linke Dreieck: Die Strecke \(|AH_b| = c/2\) (klar -warum?). Und die Strecke \(|H_bH|\) ist dann
$$|H_bH| = |AH_b| \cdot \tan 15° = \frac{c}{2} \cdot (2-\sqrt{3})$$ und die Strecke \(|H_bC| = \sqrt{3} \cdot |H_bH|\). Daraus folgt dann die Fläche des Dreiecks \(\triangle H_bHC\).
$$F(\triangle H_bHC) = \frac12 |H_bH| \cdot |H_bC| \\ \space =\frac{\sqrt{3}}{2} \left( \frac{c}{2} \cdot (2-\sqrt{3}) \right)^2 = \frac{\sqrt{3}}{2} \cdot \frac{c^2}{4}(2-\sqrt{3})^2$$ Die Summe beider Dreiecke gibt die Fläche \(F\) des Vierecks:
$$F = \left( 1 + \frac{\sqrt{3}}{2} \right) \frac{c^2}{4}(2 - \sqrt{3})^2 \\ \space = \left( 1 + \frac{\sqrt{3}}{2} \right) \frac{c^2}{4} (7 - 4\sqrt{3}) = \frac{c^2}{8}(2-\sqrt{3})$$ Gruß Werner