Alpha rechnerisch bestimmen

Question

ich soll diese Aufgabe rechnerisch lösen. Alpha soll bestimmt werden. Die Informationen dazu sollen aus dem Bild heraus gehen. Ich bedanke mich schon jetzt für eure Bemühungen.

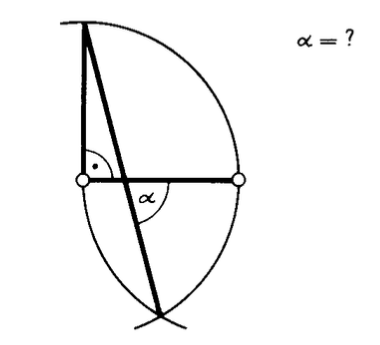
Die Aufgabe stammt von P.Eigenmann ( Stuttgart: Klett 1981)

Ohne Taschenrechner; die Figuren sind nicht maßgetreu.

Paul Eigenmann, Aufgabe 1.1.27, ISBN 3-12-722310-2, 1981, S. 7.

Answer 1

Lege das Ganze in  ein Koordinatensystem mit (0|0) als Mittelpunkt eines Kreises mit dem Radius 1. Dann scheidet eine Gerade g die x-Achse im Winkel β, sodass α+β=180°. Die Gerade geht durch (0|1) und ( 1/2|-√3/2) und hat folglich die Steigung -(√3+2)=tan(β). Dann ist β=105°und α=75°.

Comments

Wenn ich das richtig überblicke, ist die von dir angegebene Steigung nicht tan(β), sondern tan(α).

Schöne Aufgabe und gute Lösung!

---

Danke für die Bewertung "gute Lösung".Ich habe α=75° angegeben. DenTangens davon erwähne ich nirgends.

---

Hallo Roland,
woher hast du den Punkt
( 1/2 | -√3/2 )  ?
mfg Georg

Ich sehe nunmehr das vom linken
punkt ein weiteres Kreis geschlagen
wurde.

Meine Frage wird dadurch beantwortet.

---

(√3+2)=tan(β).

Das ist aber tan(α).

---

Einfacher ohne Trigonometrie oder Koordinatensystem :

γ = β  (Basiswinkel im gleichschenkligen Δ DEA)
δ = β  (Wechselwinkel an Parallelen EF und BD)
γ + δ =  30°  (EF ist Höhe im gleichseitigen Δ DEC)
⇒  δ = 15°

⇒  α = 75°  (Winkelsumme im rechtwinkligen Δ GEF)

---

@willyengland: Dein TR zeigt immer nur einen Wert. α und β haben den gleichen Tangens.

@georg: Deine Frage wird auch durch die Skizze von hl2166 beantwortet, der offenbar dazu übergeht, nicht nur kryptische Andeutungen zu machen.

---

Hallo Roland,
75 ° habe ich auch heraus.
Sobald der Punkt ( 1/2 | -√3/2 ) 
berechnet ist genügt eine
etwas einfachere Skizze zur Lösung.

Fällt mir gerade auf : in der Skizze muß es
auch -√3/2 heißen.

mfg Georg