Hallo Marco,
mit der Normalenform ist es einfach. Zunächst eine Skizze (ohne Skizze geht in Vektorrechnung gar nichts!)
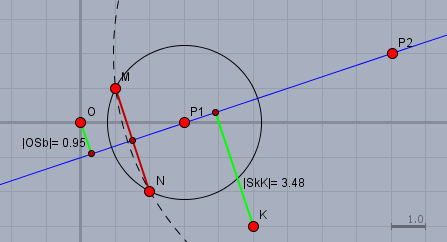
Dort siehst Du die Punkte \(M\), \(N\) und \(K\). Die (blaue) Mittelsenkrechte der Strecke \(MN\) ist die Menge aller Punkte, die von beiden Punkten den gleichen Abstand haben. Ich habe Dir stellvertretend zwei Punkte \(P_1\) und \(P_2\) eingezeichnet. Zieht man einen Kreis um einen der beiden Punkte, der durch \(M\) verläuft, so läuft derselbe Kreis auch durch \(N\).
Mit Hilfe der Normalenform lässt sich nun die Mittelsenkrechte leicht bestimmen. Die Strecke \(MN\) steht bereits senkrecht auf der Geraden, also taugt der Vektor \(\vec{MN}\) auch als Normalenvektor für die Geraden. Es ist $$\vec{MN} = \vec{N} - \vec{M}= \begin{pmatrix} 2\\-2 \end{pmatrix} -\begin{pmatrix} 1\\1 \end{pmatrix} = \begin{pmatrix} 1\\-3 \end{pmatrix}$$ Jetzt benötigen wir noch einen Punkt auf der Geraden, und dafür bietet sich der Mittelpunkt \(A\) der Strecke an. Es ist $$\vec{A} = \frac12 \left( \vec{N} + \vec{M} \right)= \frac12 \left( \begin{pmatrix} 2\\-2 \end{pmatrix} +\begin{pmatrix} 1\\1 \end{pmatrix}\right) = \begin{pmatrix} 1,5\\-0,5 \end{pmatrix}$$ Dies setze ich nun in die Normalenform $$\vec{MN} \cdot (\vec{x} - \vec{A}) = 0$$ ein und erhalte: $$\begin{pmatrix} 1\\-3 \end{pmatrix} \cdot \left(\vec{x} - \begin{pmatrix} 1,5\\-0,5 \end{pmatrix} \right) = 0 \\ \begin{pmatrix} 1\\-3 \end{pmatrix} \cdot \vec{x} - (1 \cdot 1,5 + (-3) \cdot (-0,5)) = 0 \\ \begin{pmatrix} 1\\-3 \end{pmatrix} \cdot \vec{x} - 3 = 0$$ Mache mal die Probe! Setze den Punkt \(P_1=\begin{pmatrix} 0 & 3 \end{pmatrix}^T \) ein (s. Skizze), und Du siehst, dass die Gleichung aufgeht.
Um die Abstände zu bestimmen, überführen wir die Normalengleichung in die Hessesche Normalform $$\vec{n} \vec{x} - d=0 \quad \text{mit} \space |\vec{n}|=1; \space d\ge0$$ Um den Normalenvektor auf den Betrag von 1 zu bringen, müssen wir ihn durch seine Länge teilen. $$\vec{n} = \frac{\vec{MN}}{|\vec{MN}|} = \frac{1}{\sqrt{1^2 + (-3)^2}}\begin{pmatrix} 1\\-3 \end{pmatrix} = \frac{1}{\sqrt{10}}\begin{pmatrix} 1\\-3 \end{pmatrix}$$ Dasselbe müssen wir mit \(d\) machen, sonst stimmt die Gleichung nicht mehr. Also dividiere ich alles durch \(\sqrt{10}\). $$\frac{1}{\sqrt{10}}\begin{pmatrix} 1\\-3 \end{pmatrix} \cdot \vec{x} - \frac{3}{\sqrt{10}} = 0 \\$$ Diese Form hat den Vorteil, dass man damit unmittelbar die Abstände von anderen Punkten zu dieser Geraden berechnen kann. $$\begin{aligned} d(s,O) &= \left|\frac{1}{\sqrt{10}}\begin{pmatrix} 1\\-3 \end{pmatrix} \cdot \vec{O} - \frac{3}{\sqrt{10}}\right| \\ &= \left|\frac{1}{\sqrt{10}}\begin{pmatrix} 1\\-3 \end{pmatrix} \cdot \begin{pmatrix} 0\\0 \end{pmatrix} - \frac{3}{\sqrt{10}}\right| \\ &= \frac{3}{\sqrt{10}} \approx 0,95\end{aligned}$$ $$\begin{aligned} d(s,K) &= \left|\frac{1}{\sqrt{10}}\begin{pmatrix} 1\\-3 \end{pmatrix} \cdot \vec{K} - \frac{3}{\sqrt{10}}\right| \\ &= \left|\frac{1}{\sqrt{10}}\begin{pmatrix} 1\\-3 \end{pmatrix} \cdot \begin{pmatrix} 5\\-3 \end{pmatrix} - \frac{3}{\sqrt{10}}\right| \\ &= \frac{11}{\sqrt{10}} \approx 3,48\end{aligned}$$ Kontrolliere das Ergebnis in der Skizze.
Gruß Werner