Quadrat mit Umkreis und Winkel - Beweis einer Parallelität

Question

Quadrat mit Umkreis und Winkel - Beweis einer Parallelität

2 Antworten

Ein anderes Problem?

Werner-Salomon · Answer 1 · 2019-03-09T19:17:27+0000

Hätte man das Ganze eigentlich auch mit Vektoren beweisen können?

Ja - das geht sogar ziemlich 'straight forward'. D.h. es ist eine ziemliche Rechnerei, aber eben "nur" eine Rechnerei. Im Gegensatz zum 'geometrischen' Beweis - wie in der Antwort von hj2166, der eine gewisse Kreativität erfordert!

Ich nenne $\vec{AB} = a$ und $\vec{AD} = b$ . Der Vektor $\vec{BN} = \tau b$ mit $\tau \in \mathbb{R}$ . Die Idee ist nun, sowohl den Vektor $\vec{NM}$ als auch $\vec{PQ}$ zu berechnen und dann zu zeigen, dass beide unabhängig von $\tau$ kollinear sind. Ich führe noch eine Funktion $o$ (für orthogonal) ein, wobei $o(x)$ der um 90° positiv gedrehte Vektor von $x$ ist. Es gilt also $b=o(a)$ und $o(b)=-a$ .

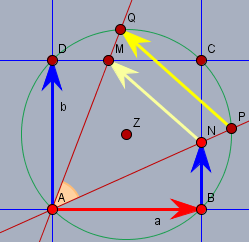
Ich wähle den Punkt $A$ als 'Ursprung'. Dann sind die Geraden $g_0$ und $g_1$ durch $AN$ und $AM$ $g_0: \space x = s (a+\tau b), \quad s \in \mathbb{R}\\g_1: \space x = t (a+ \tau b + o(a+\tau b)) = t(a(1-\tau) + b (1+\tau)), \quad t \in \mathbb{R}$ Damit berechne ich die Vektoren $\vec{AN}=n$ und $\vec{AM}=m$ . $n$ ist offensichtlich $n = a+\tau b$ und $m$ ist der Schnittpunkt von $g_1$ und $g_2: \space x = b + ra$ Gleichsetzen gibt $\begin{aligned}ta(1-\tau) + tb (1+\tau) &= b + ra \\ (t(1 - \tau) - r)a + (t (1 + \tau) - 1)b &= 0\end{aligned}$ Da $a$ und $b$ linear unabhängig sind, müssen die Faktoren =0 sein. Aus dem Faktor vor $b$ folgt direkt $t_m (1+\tau) - 1 = 0 \implies t_m = \frac{1}{1 + \tau}$ und damit der Vektor $m$ : $m = g_1(t_m) = \frac 1{1 + \tau}(a(1-\tau) + b (1+\tau))= a \frac{1-\tau}{1 + \tau} + b$ Somit ist der Vektor $\vec{NM}$ $\vec{NM} =m-n = a \frac{1-\tau}{1 + \tau} + b - a-\tau b = a \frac{-2\tau}{1+\tau} + b(1-\tau)$ Ist $k$ ein beliebiger Vektor von $A$ auf die Kreislinie und $z=\vec{AZ}$ , so ist $(k-z)^2 = z^2, \quad z = \frac 12 (a+b) \\ k^2 - 2kz + z^2 = z^2 \\ k^2 = k(a+b)$ Den Kreis bringe ich mit $g_0$ und $g_1$ zum Schnitt, um die Vektoren $\vec{AP} = p$ und $\vec{AQ} = q$ zu bestimmen. Dazu setzt man für $k$ die Gleichung der jeweiligen Gerade ein. Zunächst $g_0$ für $p$ : $\begin{aligned} s^2 (a + \tau b)^2 &= s(a + \tau b)(a+b) \\ s(a^2 + 2\tau ab + \tau^2 b^2) &= a^2 + ab(1+\tau) + \tau b^2 \\ s a^2(1 + \tau^2) &= a^2( + \tau) \\ s_p &= \frac {1 + \tau}{1 + \tau ^2} \end{aligned}$ Dann $g_1$ für $q$ : $\begin{aligned}t^2(a(1-\tau) + b (1+\tau))^2 &= t(a(1-\tau) + b (1+\tau))(a+b) \\ t(a(1-\tau) + b (1+\tau))^2 &= (a(1-\tau) + b (1+\tau))(a+b) \\ t( a^2(1-\tau)^2 + b^2 (1+\tau)^2) &= a^2 (1-\tau) + b^2 (1+\tau) \\ t( 1+\tau^2) &= 1\\ t_q &= \frac 1{1+\tau^2}\end{aligned}$ Und nun die Differenz $\vec{PQ}$ : $\begin{aligned} \vec{PQ} &= q-p = g_1(t_q) - g_0(s_p) \\ &= \frac 1{1+\tau^2}(a(1-\tau) + b (1+\tau)) - \frac {1 + \tau}{1 + \tau ^2} (a+\tau b) \\ \quad &= \frac 1{1 + \tau ^2} \left( a(1-\tau) + b (1+\tau) - (1 + \tau )(a+\tau b)\right) \\ \quad &= \frac 1{1 + \tau ^2} \left( -2a\tau + b (1-\tau^2) \right) \\ \quad &= \frac {1+\tau}{1 + \tau ^2} \left( a \frac{-2\tau}{1+\tau} + b (1-\tau) \right) \\ \quad &= \frac {1+\tau}{1 + \tau ^2}\vec{NM} \quad \text{q. e. d.} \end{aligned}$

Gast hj2166 · Answer 2 · 2018-11-30T00:15:32+0000

1. β = 2α (Zentrums-Peripherie-Winkel-Satz)

2. γ = (180° - β) / 2 (Satz vom gleichschenkligen Dreieck)
γ = 90° - α (wegen 1.)

3. δ = ∠BAZ - ∠PAZ
        = 45° - ∠PAZ (Satz vom gleichschenkligen Dreieck)
         = ∠PAQ - ∠PAZ (Voraussetzung)
         = γ
         = 90° - α (wegen 2.)

Konstruktion : Das Quadrat ABCD wird um 90° um den Punt A gedreht.

4. ε + δ' = ε + δ (Konstruktion)
                = 90° - ∠NAM
                = 90° - 45° (Voraussetzung)
                = 45°
                = ∠NAM (Voraussetzung)

AN = AN' (Konstruktion)

5. ΔNAM ≅ ΔN'AM (Kongruenzsatz SWS wegen 4.)

6. η = ζ (wegen 5.)
        = 90° - δ' (wegen Quadrat)
        = 90° - δ (Konstruktion)
        = α (wegen 3.)

7. PQ || NM (Stufenwinkelsatz wegen 6.)

Quantenelektrodynamik.

Kommentiert 5 Mär 2019 von Gast hj2166

Quadrat mit Umkreis und Winkel - Beweis einer Parallelität

2 Antworten

Ähnliche Fragen

Eingabetools:

Beliebte Fragen:

Heiße Lounge-Fragen: