Einheiten km und h.
Anmerkung vorweg: Wegen der kurzen Distanz kommt weniger als 1 h Fahrzeit raus.
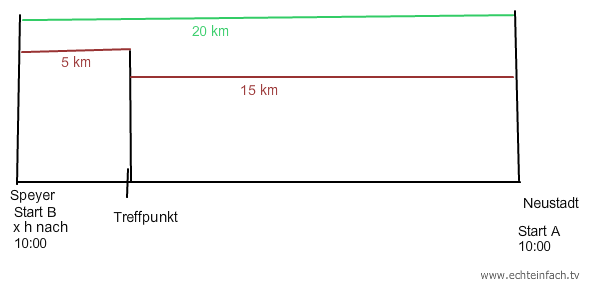
A fährt mit 20 km/h. d.h.
in 1 h 20 km
in 2 h 40 km
in y h Fahrzeit 20*y km
man weiss aus der Skizze 20*y = 15 → y = 3/4 h = 45 Min.
B fährt mit 18 km/h. d.h.
in 1 h 18 km
in z Stunden Fahrzeit 18*z km
man weiss aus der Skizze 18*z = 5 → z = 5/18 h = 16.666… Min.
Du kannst eine Gleichung zur Wartezeit von B machen:
x + z = y
und hier die Fahrzeiten einsetzen
x + 5/18 = 3/4 |-5/18
x = 3/4 - 5/18 = 27/36 - 10/36 = 17/36 h = 28.3333… Min = 28 Min 20 Sek.
Also: Abfahrtszeit B: 10 Uhr 28 Min 20 Sek
Exkurs:
Beim Umrechnen von h auf Minuten rechnet man * 60.
Von 1/3 Minute auf Sekunden: Ebenfalls * 60
Aufgabe b) hat man schon aus den Zwischenresultaten.