Fragen zum Gradientenfeld und zur Richtungsableitung

Question

Die Funktion f: R^2 → R sei definiert als f(x, y) = x·y.

(a) Skizzieren Sie die Niveaulinien f(x, y) = h für die Werte h = -3; -2; -1; 0; 1; 2; 3.

f(x, y) = x·y = h
y = h/x

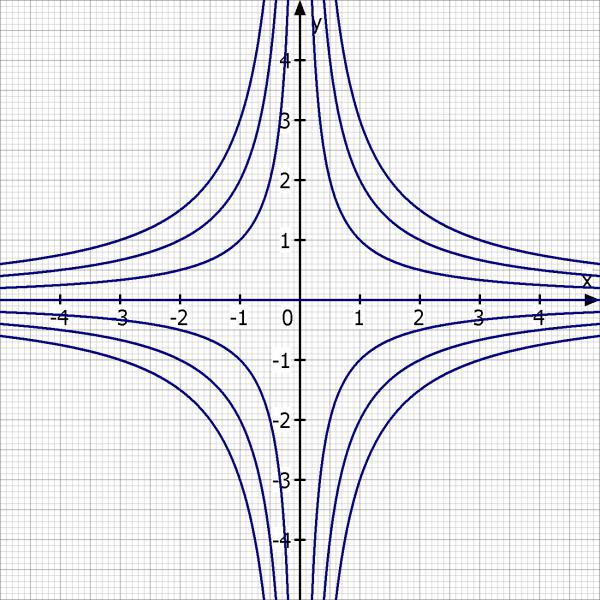
(b) Skizzieren Sie die Schnittlinien für y = 1 und y = x.

Hier ist mir nicht ganz klar was ich machen soll?

(c) Berechnen Sie sämtliche ersten und zweiten partiellen Ableitungen.

df/dx = y
df/dy = x

d^2f/dxdx = 0
d^2f/dxdy = 1
d^2f/dydx = 1
d^2f/dydy = 0

(d) Skizzieren Sie das Gradientenfeld.

Auch hier weiß ich nicht ganz genau wie ich am besten vorgehen kann.

(e) Berechnen Sie die Richtungsableitung am Punkt (1; 1) in Richtung der Vektoren (1; 1); (1; 0) und (1; -1).

Auch hier bräuchte ich noch etwas Unterstüzung.

 

Es wäre nett wenn mir da jemand auf die Sprünge helfen kann.

Comments

Meinst du so was? https://www.wolframalpha.com/input/?i=grad+sin%28x%5E2+y%29&lk=3

Wie man das am Compi zeichnet, weiss ich nicht. Du kannst von Hand vielleicht einfach Pfeilchen ±senkrecht an die Niveaulinien kleben, die dann in die richtige Richtung schauen.

Answer 1

Hi,

b) Da bin ich selbst nicht ganz sicher. Habs auch kurz gegooglet. Ist kein bekannter Begriff (zumindest find ich nix).

Kannst ja zur Not die beiden Geraden einzeichnen :P.

 

d)

grad f = (y,x)

Nun einfach einen Punkt wählen (Bspw. P(1,1))

Der Gradient in P ist nun auch (1,1) (also einsetzen in grad f). Den Vektor abtragen und Du hast den ersten Schritt zur Zeichnung getan.

 

e)

Für die Richtungsableitung:

D(f) = grad f(1,1) * v/||v||

v ist dabei der Richtungsvektor

 

Grüßle

Comments

Ok. Soweit hab ich das denke ich verstanden. Warum schreibst Du

D(f) = grad f(1,1) * v / ||v||

Ist das der Betrag von v? Warum die doppelten Betragsstriche?

---

Ja, das ist eigentlich nur der Betrag.

Oder die Norm. Glaub wir hatten das damals mit zwei Betragsstrichen ist aber in unserem Fall das Gleiche (da 2-Norm).