In eine Schublade befinden sich 4 schwarze, 6 blaue und 2 grüne Socken. Es werden zufällig zwei Socken entnommen.
Das Baumdiagramm dazu sieht so aus:
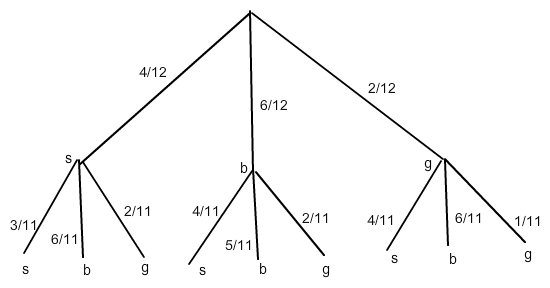
Ich habe das Bild von -Wolfgang- geklaut.
1.Pfadregel: Entlang eines Pfades von der Wurzel (oben) bis zum Blatt (unten) multiplizieren und die Wahrscheinlichkeit eines Pfades zu berechnen.
Beispiel. Die Wahrscheinlichkeit, dass die erste Socke blau und die zweite grün ist, ist also \(\frac{6}{12}\cdot\frac{2}{11} = \frac{1}{11}\)
2.Pfadregel (auch Summenregel genannt): Die Wahrscheinlichkeiten der einzelnen Pfade werden addiert.
Beispiel. Die Wahrscheinlichkeit, dass eine socke blau und die andere grün ist setzt sich zusammen aus
- der Wahrscheinlichkeit, dass die erste Socke blau und die zweite grün ist. \(\frac{1}{11}\), s.o.,
- der Wahrscheinlichkeit, dass die erste Socke grün und die zweite blau ist. \(\frac{2}{12}\cdot\frac{6}{11} = \frac{1}{11}\).
Die Wahrscheinlichkeit, dass eine Socke blau und die andere grün ist, ist also \(\frac{1}{11}+\frac{1}{11} = \frac{2}{11}\).