Stetigkeit in normierten Vektorräumen, Probleme bei Abschätzungen

Question

Text erkannt:

(1) Untersuchen Sie, in welchen Punkten $a \in \mathbb{R}^{3}$ die Funktion $f$ stetig ist:
(a) $f: \mathbb{R}^{3} \rightarrow \mathbb{R}:(x, y, z) \mapsto\left\{\begin{array}{cl}0 & \text { für }(x, y, z)=(0,0,0) \\ \frac{x y z}{|x|+|y|+|z|} & \text { für }(x, y, z) \neq(0,0,0)\end{array}\right.$
(b) $f: \mathbb{R}^{3} \rightarrow \mathbb{R}:(x, y, z) \mapsto\left\{\begin{array}{cl}0 & \text { für }(x, y, z)=(0,0,0) \\ \frac{x y z}{x^{2}+y^{2}+z^{2}} & \text { für }(x, y, z) \neq(0,0,0)\end{array}\right.$
(c) $f: \mathbb{R}^{3} \rightarrow \mathbb{R}:(x, y, z) \mapsto\left\{\begin{array}{cl}0 & \text { für }(x, y, z)=(0,0,0) \\ \frac{x y z}{|x|^{3}+|y|^{3}+|z|^{3}} & \text { für }(x, y, z) \neq(0,0,0)\end{array}\right.$

Die Aufgabe lautet wie folgt:

Die Aufgabe 1a) konnte ich bereits lösen. Für die "Nicht kritischen Punkte" bzw. (x,y,z) != (0,0,0) habe ich mit stetigen Funktionen argumentiert und beim Punkt (0,0,0) habe ich mit der Epsilon-Delta Definiton der Stetigkeit gearbeitet, bzw. abgeschätzt und bin auf ein passendes Epsilon gekommen. Hier meine Notizen:

Text erkannt:

fall 2 ) $(x, y, z)=(0,0,0)$
Wir verwenden die summennorm $\|\times\|_{1}$

Nun bin ich bei Aufgabe 1b) und komme beim abschätzen nicht weiter... Hier mein Ansatz:

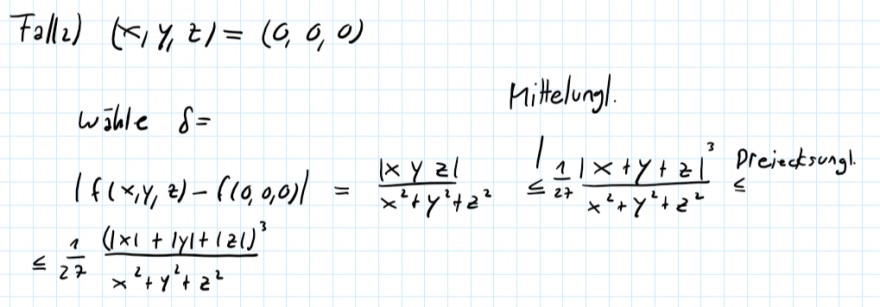
Text erkannt:

$\left.F_{2} \|_{2}\right)(x, y, z)=(0,0,0)$
wible $\delta=$
$$\begin{array}{l}\mid f(x, y, z)-\left((0,0,0) \mid=\frac{|x y z|}{x^{2}+y^{2}+z^{2}} \leq \frac{1}{27} \frac{|x+y+z|^{3}}{x^{2}+y^{2}+z^{2}}\right. \\ \leq \frac{1}{27} \frac{(|x|+|y|+|z|)^{3}}{x^{2}+y^{2}+z^{2}}\end{array}$$

Bin ich auf dem richtigen Weg oder vertue ich mich da?

Answer 1

Hallo,

zunächst ein Hinweis: Du musst bei der Mittelungleichung von Anfang an mit Beträgen abschätzen. Die Ungleichung

$$|xyz| \leq \frac{1}{3}|x+y+z|$$

stimmt so nicht.

Was die zweite Aufgabe angeht. Du kannst verwenden, dass

$$|x| = \sqrt{x^2} \leq \sqrt{x^2+y^2+z^2}=\|(x,y,z)\|_2 \text{ (euklidische Norm)}$$

Analog natürlich für die anderen Komponenten.

Bei der 3. Aufgabe würde ich mal auf $f(x,x,x)$ schauen.

Noch ein allgemeiner Tipp: Konvergenz im $\mathbb{R}^n$ ist äquivalent zur komponentenweisen Konvergenz, also

$$(x_n,y_n,z_n) \to (0,0,0) \iff x_n \to 0, y_n \to 0, z_n \to 0$$

Die Grenzwertsätze für Folgen in Kombination mit Abschätzungen sind oft einfacher zu verwenden, als die epsilon-delta-Konstruktion.

Gruß Mathhilf

Comments

Danke vielmals! Sie haben mir sehr geholfen.

Ich habe die 1b) nun so gelöst:

Text erkannt:

$\left.F_{2} \|_{2}\right) \quad(x, y, z)=(0,0,0)$
woble $\delta=\varepsilon$
$B_{\varepsilon}\left(f(0,0,0)=\left\{f(x, y, z) \in \mathbb{R} \mid\left\|f\left(x, y_{z}\right)\right\|_{2}<\varepsilon\right\}\right.$

Und die 1c) wie folgt:

Ich glaube das müsste so passen oder?

Freundliche Grüsse

Migsan

---

Ah und wäre die Mittelungleichung so richtig angewandt?

|xyz| <= (1/27)*(|x|+|y|+|z|)³

---

Hallo,

ja, das sieht alles gut aus.

Gruß Mathhilf